
Assignment 1
By: J. Matt Tumlin, Cara Haskins, & Robin Kirkham
Examine graphs of y = a sin(bx
+ c) for different values of a, b, and c.
Our first step will be to look
at the basic sine graph
when a=1, b=1 and c=0.
![]()
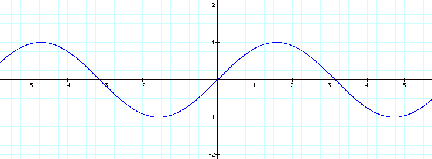
Notice that the Domain is the set of real numbers, and
the Range is [-1,1]. The graph of the sine function continues indefinitely.
The amplitude is the distance
from the axis to the highest or lowest point, or it is half the distance from
the highest to the lowest point.
Let us use during this example the variable ÒaÓ in demonstrating the
amplitude which is currently a = 1.
The period is the time it takes
for the graph to make one complete cycle or in other words, the amount of time
it takes for the graph to begin repeating. Let use the variable ÒbÓ in conjunction with adjusting the
period. In this case the period is
2p.
In our example, the sine wave
phase is controlled by the variable ÒcÓ.
Which in this first case, c = 0.
Continue to use the basic sine
graph as our frame of reference. Let us examine what happens to the graph under
the following guidelines.
Step 1: a sin (bx +c)
Let b=1,c=0, and vary the
values of a. Our new equation becomes
y=a sin(x).
Let us use Graphing Calculator
3.2 to examine the effects of using different values for a , remembering to use
positive and negative values.
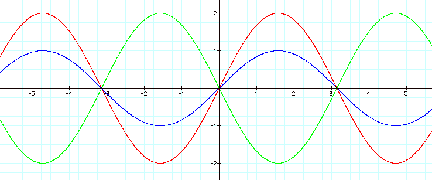
The blue graph is y=sin x. This
basic sine graph will always be in blue in future examples for comparison purposes.
Notice when the value for ÒaÓ
is
positive, the amplitude increases by a factor of the absolute value of
"a", and the graph emulates the y = sin x graph as
demonstrated above. This is known as a vertical stretch. Similarly, when the
variable "a" is negative, the amplitude is still increased by the
absolute value of ÒaÓ. However, the negative value of "a" causes the
graph to be reflected across the
x-axis.
Step 2: Now we
are examining the effects of variable ÒbÓ. Let a=1, and c=0 and change the values for b. Our new equation is now:
y = sin (bx).
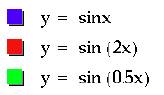
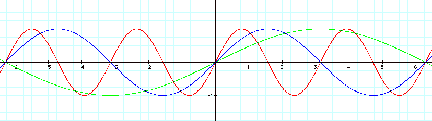
Notice that
the amplitude of the graphs does not change even though the value for b was
varied. When ÒbÓ > 1, the
period of the graph is changed to 2p/b, resulting in
a horizontal shrinking of the graph.
When 0 < ÒbÓ < 1, then the period is still changed to 2p/b, however the graph is now stretched.
This leaves
the question what happens when negative values are substituted for variable
ÒbÓ?
By substituting
negative values for ÒbÓ, notice there is a reflection across the x-axis for our
two graphs as well as a horizontal change of the basic sine graph.
Step 3: Let us start again with our original equation y= asin(bx+c). Let a=1, b=1, and vary c, resulting in:
y = sin(x+c)
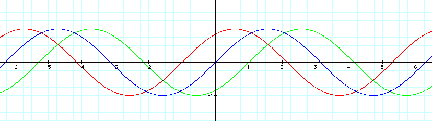
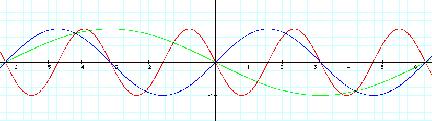
The value of
variable ÒcÓ moves the sine graph to the right or the left. When ÒcÓ > 0,
the graph moves to the left. When
ÒcÓ < 0, the graph moves to the right.
This
horizontal movement is called the phase shift. The phase shift appears to be equal to the value of Ò-cÓ.
To be sure,
let us check what happens to a change of variable ÒbÓ and ÒcÓ simultaneously.
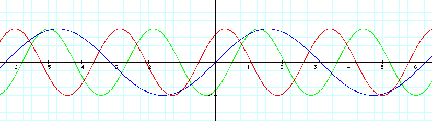
This shows us
that phase shift is effected by ÒbÓ.
Thus, the phase shift is actually ÒÐc/bÓ.
In summary, given
the equation y = a sin (bx +c) the following are true:
á Changes in the
value of ÒaÓ effects the altitude of the sine graph.
á Changes in the
value of ÒbÓ effects the period of the graph.
á Changes in the value
of ÒcÓ in conjunction with the value of ÒbÓ together effect the phase shift of
the graph.