
Polar
Equations
(Assignment 11)
by
J. Matt Tumlin, Cara Haskins, and Robin Kirkham
Through the assistance of
Graphing Calculator 3.2, we investigate the different variances when graphing
Polar equations.
Explore the equation r
= a + b cos (k q) such that 0 £ q £ 2 p
Since there are three
variables a, b, and k to explore, there are many cases to explore.
1.
When
a and b are equal, and k is an integer, this is referred to
as the “n-leaf rose.”
Let us graph such that :
a = b = 2, k = 1 (red)
a = b = 4, k = 1 (green)
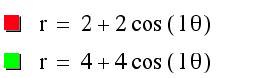
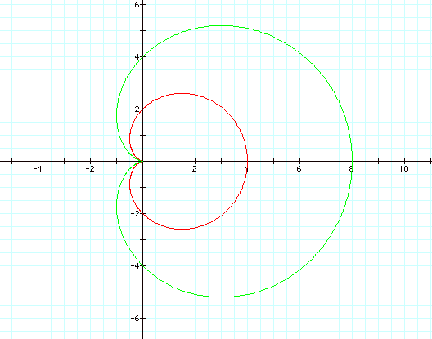
Notice that when a=b , a
and b are scalar factors for the “n-leaf rose”. Also, when k=1, the roots of r = a + b cos (k q) are 0 and a+b.
Next, we observe the
effect of k on the equation.
Below are the graphs of:
a = b = 2, k = 3 (red)
a = b = 4, k = 5 (green)
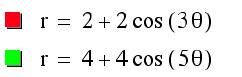
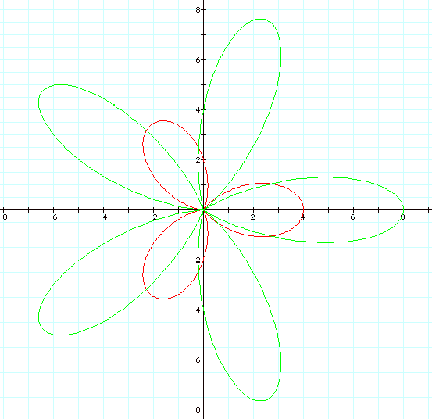
With these graphs and
further exploration, we observe that k determines the number of leaves in the
“n-leaf rose” figure.
2. Let’s now look at the
graph of a=2, b=8, and k=1.
![]()
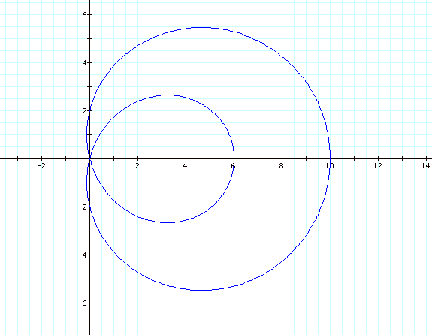
When a < b and k is an integer, r = a + b cos (k q) have roots at 0, a+b,
and a-b.
When a< b, the function traces a similar path to the
“n-leaf rose” graph, but not on the same scale.
It appears that the results provide a “k-leaf rose”.
One inner “leaf” always is at b-a on the x-axis.
3.
What
happens when a > b and k is an integer?
To see, let’s investigate
the graph of a = 5, b= 2, and k= 10.
![]()
The “leaves” are merging
towards a circle form.
The leaves come into a point
on the circle centered on the origin with the radius a-b.
The tips of the leaves
work out to a point on the circle centered at the origin with the radius a+b.
The function oscillates
between these two circles k times to produce k “leaves”.
Once k becomes large
enough, other characteristics can be explored.
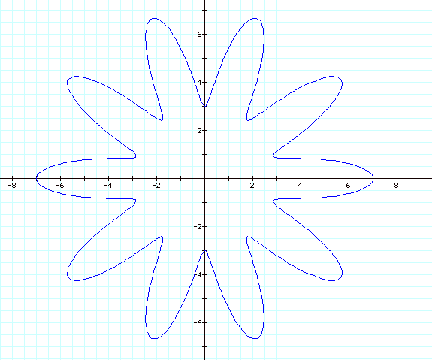
Look at a=5, b= 4, and
k=1000
![]()
This graph has many
different characteristics that could be explored. Observe that the center is
not filled.
Notice that there is a five
leaf rose in the center as well as the outer leaves (if you will) are also
five.
This seems to be related
to the “a” value.
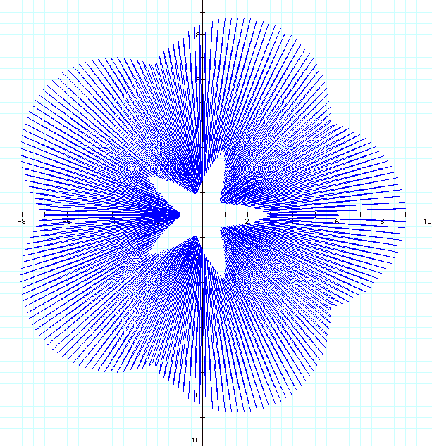
![]()

When k=2000 is tried,
notice that the internal number of leaves becomes 10.
With some further
investigation it seems that the number of leaves is “1000/200 = 5”.
4. What about when a = b and k is NOT an
integer?
Let a = b = 5, and k = 3 (green)
and a = b = 5, and k = 3.4 (red)
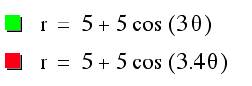
Observe that the graph is
no longer continuous.
The two graphs are merging
towards each other.
Thus, only when k is an
integer is the graph continuous.
When k is between 3 and 4
then the number of leaves is also between three and four.
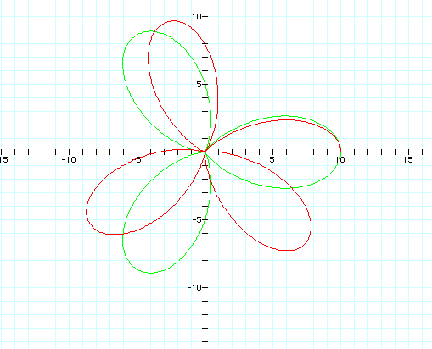
5.
When
a < b and k is not an integer, what occurs?
When a < b and k is not
an integer, observe a similar transformation taking place as we witness when
a=b and k is not an integer.
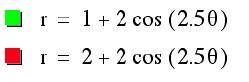
As observed before there
are between 2 and 3 leaves due to k being not an integer.
6.
How
about when a > b and k is not an integer.
When a > b and k is not
an integer, what do you think is observed this time?
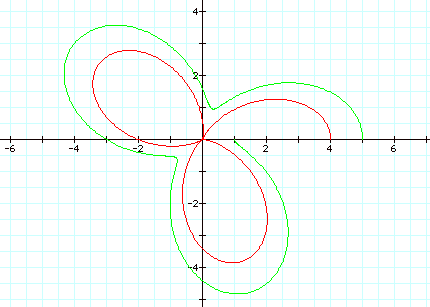
Conclusion:
Š
As
a, b, and k vary there seems to be many relationship issues that can be
discussed. The number of leaves and the relationship that both a and b have
seem to be related.
Š
It
becomes more interesting when the values are no longer integers, that is when
all the changes and predictions change.
This looks like an
investigation that can be shared with high school students allowing them to draw
quite a few different and interesting conclusions as well as what has been
observed.