
Tangent
Circles
(Assignment 7)
by
J. Matt Tumlin, Cara Haskins, Robin Kirkham, and Audrey
Simmons
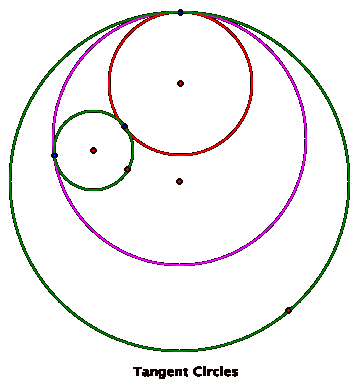
Let us consider the problem of having two circles whereas one is inscribed within the other, and a third circle is constructed such that it is tangent to both the original circles.
We are given :
Two circles
A point on one
of the circles
Let us start
with two circles below shown in green.
We add the red
circle inside the large green circle keeping it outside of the smaller green
circle. The red circle has been constructed using the point on the outer
circle.
When adding
the purple circle tangent to the larger green circle we observe that there is
no tangency to the smaller circle.
The purple circle is constructed to circumscribe the smaller green
circle.

To use the
tangent circle script click HERE!
Loci of the centers of the tangent circles
If we look at
the loci of the centers of the red tangent circle, what shape would be
graphed? To see click HERE!
If we look at
the loci of the centers of the purple tangent circle, what shape would be
graphed? To see click HERE!
Each set of
loci makes a separate ellipse.
Loci of the
base of the isosceles triangle
Review the
construction of the red tangent circle, the one that was externally tangent to
the small green circle (above).
Segment AB is
the base of an isosceles triangle. It is apparent that all points on the dotted
red line are equidistant from both point A and B since the line is the
perpendicular bisector of AB.
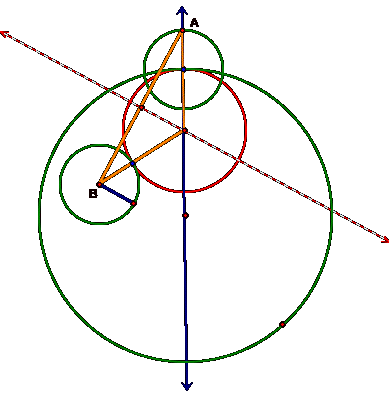
Can you guess what shape would be made with the trace of the loci of the midpoint of the base of the isosceles triangle? Instead of making an ellipse, the loci of the midpoints is a ________?
(Try this and
see)
To look at the
locus of the midpoint of the segment, click HERE!
Notice that
the locus of the midpoints of the purple circle is also the same.
The
consistency of the arrangement of the points is quite interesting.
Conclusion: In
summary, the loci of the centers of the tangent circles form ellipses. The loci
of the midpoints of the base of the isosceles triangle (while under
construction) form circles.