Final Assignment

by

J. Matt Tumlin

PART A

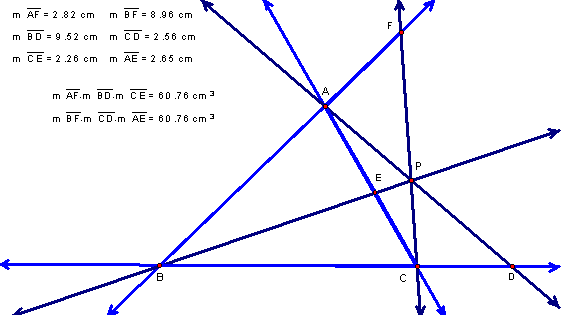
Consider any triangle ABC.  Select point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points, D, E, and F respectively.

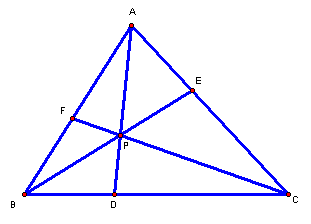
Explore (AF)(BD)(CE) and (BF)(CD)(AE) for various triangles and various locations of P.

To begin, we will pick various locations of point P to see what affect it has on the relationship of the segments of the sides of the triangle. If we multiply the length of the following sides together, what occurs?

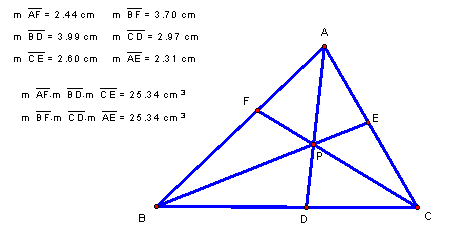
To move A, B, C, and P around, CLICK HERE!

When point P is the centroid, triangle ABC is divided into six triangles with equal area. Points D, E, and F are midpoints of ∆ABC and point P is the point of concurrency. Therefore, if we multiply the length of the following sides together, does the same thing happen?

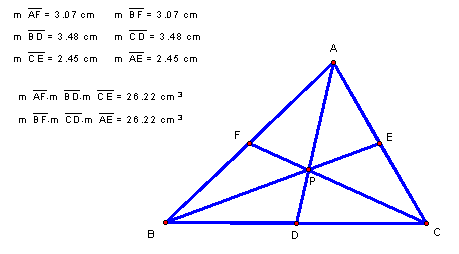
CLICK HERE to move points A, B, and C around the centroid, P.

PART B

A conjecture drawn by this manipulation is that (AF)(BD)(CE) = (BF)(CD)(AE), or .

To prove this, let’s start by extending the lines BE and CF until they meet at GH, which is through A and parallel to BC.

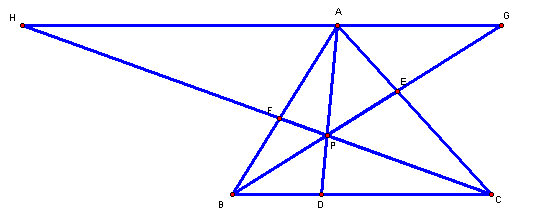
There are several pairs of similar triangles: ∆AFH, & ∆BCF, and ∆AEG, & ∆BCE, also ∆AGP, & ∆BDP, as well as ∆CDP, & ∆AHP.

From these, we can derive the following proportions:

, , , and .

Since and , then .

Therefore, .

By multiplying three of these identities together, we get:

.

Therefore, we find that:

.

Therefore, if the lines AD, BE and CF intersect at a single point P, the identity does hold.

Does this identity hold regardless of where P is located?

To use GSP, CLICK HERE!

PART C

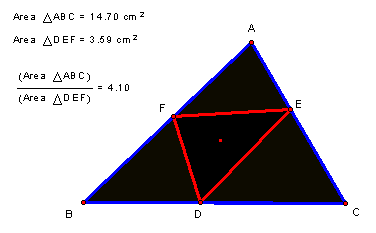
Looking back at triangle ABC and arbitrary point P inside the triangle, we can see through the GSP construction that the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4.

To move point P to different locations inside the triangle and watch the value of the ratio, CLICK HERE!

The ratio is equal to four only when D, E, and F are the midpoints of triangle ABC and point P is concurrent with the centroid of the triangle. We then have a medial triangle formed by the points.  To move A, B, and C around the centroid, CLICK HERE!

Return to Matt’s Homepage