
Final Assignment
By: Kimberly Young
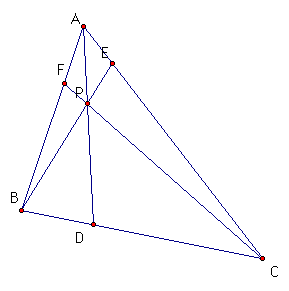
Consider any triangle ABC.
Select a point P inside the triangle and draw lines AP, BP, and
CP extended to their intersections with the opposite sides in
point D, E, and F respectively.
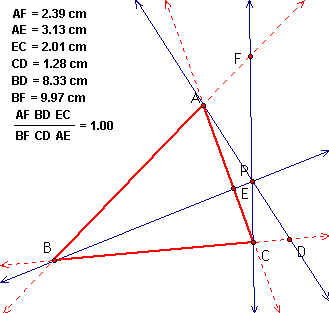
To begin to investigate, I
measured the segments, AF, BD, CE, BF, DC, and AE. With these
measurements, I then found the ratio as follows:
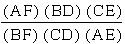 .
.
From the measurements, I found
the ratio for the triangle I constructed is 1. I also found that
when I moved point P and/or changed the size of the triangle the
ration remained 1. Click Here to
see for yourself. Below is an example.
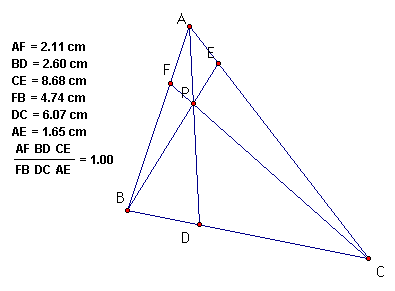
Is it true that this will always
be the case?
Prove 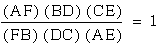 .
.
I. Consider the same construction
as we began with. Lets construct a line through point P and parallel
to segment AB. As shown below.
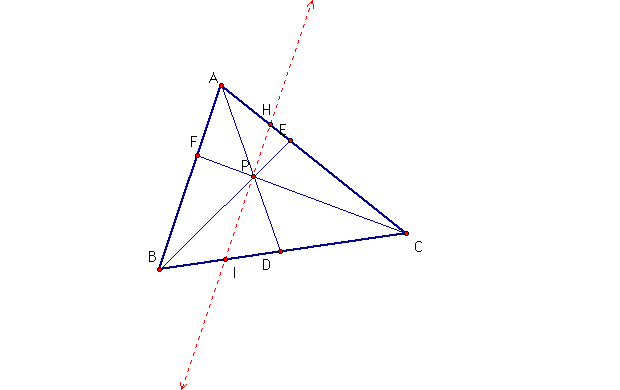
1. It follows from the construction
of the parallel line that angle AFC is congruent to angle HPC,
and angle FAC is congruent to angle PHC (by corresponding angles).
This implies that triangle AFC is similar to triangle HPC. Since
triangle AFC is similar to triangle HPC, this implies that 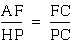 .
.
2. We also know that angle
CFB is congurent to angle CPI and angle CBF is congruent to angle
CIP (by corresponding angles). This implies that triangle CFB
is similar to triangle CPI. It follows that 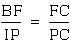 .
.
3. From 1 and 2 we have 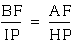 , transitive property of equality. We could
also write this as:
, transitive property of equality. We could
also write this as: 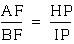 .
.
4. Also from the construction,
we have angle ABE=angle HEP. We also know, by corresponding angles
that angle ABE is congruent to HPE. This implies that triangle
ABE is similar to triangle HPE, by angle-angle similarity. It
follows that 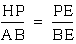 .
.
5. Also from the construction,
we have angle ADB=angle PDI. We also know, by corresponding angles
that angle BAD is congruent to IPD. This implies that triangle
BAD is similar to triangle IPD, by angle-angle similarity. It
follows that 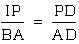 .
.
Conclusion Part I:
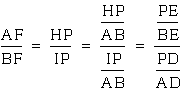 .
.
II. Construct a parallel line
through point P parallel to BC.
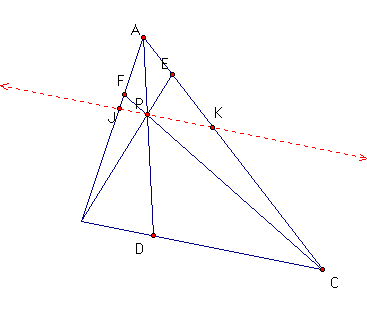
1. Through similar arguments
as before, we will see that triangle ABD is similar to triangle
AJP and triangle DAC is similar to triangle PAK. These yield
the following equalities:
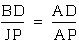
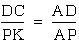
This implies 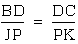 ,
which implies
,
which implies 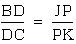 .
.
2. By the same argument, triangle
BCE is similar to triangle PKE. This gives us the following equality:
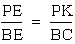 .
.
3. By the same previous argument,
triangle BCF is similar to triangle JPF. This implies that 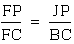 .
.
Conclusion Part II.
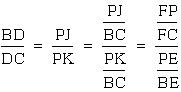
III. Consider a similar argument
for a parallel line for segment AC.
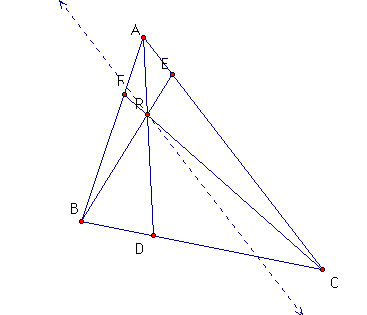
1. With this construction,
we could show as before that the following triangles are similar
and thus yield the following ratios:
a. triangle BPM is similar
to triangle BEC
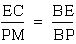
b. triangle ABE is similar
to triangle LBP
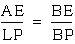
a&b imply that 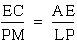 i.e.
i.e.
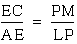 .
.
c. triangle ACD is similar
to triangle PMD
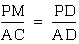
d. triangle ACF is similar
to triangle LFB
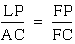
Conclusion Part III.
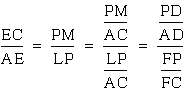
Therefore, 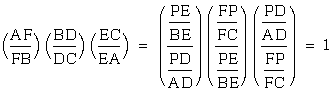 .
.
Can the result be generalized
(using lines rather than segments to construct ABC) so that point
P can be outside the triangle?
Click here to see a working GSP sketch.
Another Conjecture:
The ratio of the areas of triangle
ABC and triangle DEF is always greater than or equal to 4.
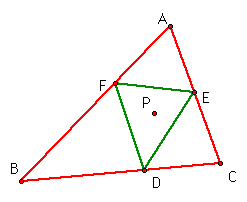
Through my investigation,
I found that the ratio of the areas of triangle ABC and triangle
DEF is equal to four when F, E, and D are the midpoints of their
corresponding sides. We know this is true because triangle DEF
forms a medial triangle. The area of the medial triangle is always
1/4 of the area of the original triangle, in our case triangle
DEF is 1/4 the area of triangle ABC.





.
.
, transitive property of equality. We could also write this as:
.
.
.
.
, which implies
.
.
.

i.e.
.
 .
.
