By watching the animation, we see that the function stretches and shrinks as the values of a change.

We also see that the function flattens out at a point and then flips, or reflects.

The question is where do these occurrences happen and at what point to they change?

To analyze these questions, consider a few graphs on the same plane.

y=(-3)sin x

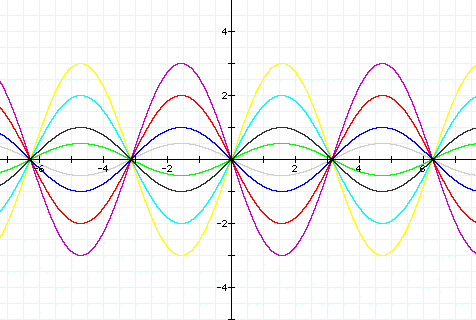
Notice the values of a change the altitude (the highest point of the function.) of the function, causing it to stretch and shrink. We can also see that the altitude directly corresponds to the value of a. In other words, we can determine the altitude of the function by the value of a. The altitude is causing the stretching and the shrinking. The function is stretched when a>1 and a<-1. It is shrunk when 1>a>-1.

It is obvious that when a=0, the function is y=0. This is what is causing the "flattening out". There something special happening when a <0, this is causing the flip of the function. When the function flips, we see that the altitude characteristics that were described above still hold.

From these results we can determine the altitude of the function y=a sin(bx+c), when b=1 and c=0. We know that the altitude of the function is a. We can also determine if the graph stretch, shrinks, flattens, and/or flips by the value of a.

Now, what happens when the values of b change for the function y=a sin (bx+c). To begin, let's take the same approach as before.

It looks like a slinky. We see the function's frequency changes as well as a reflection taking place. It seems, from the animation that the frequency is determined by the b value. Frequency is number of peaks over a given interval. The interval that we are looking at is 2 pi to 0. Consider the graph below.

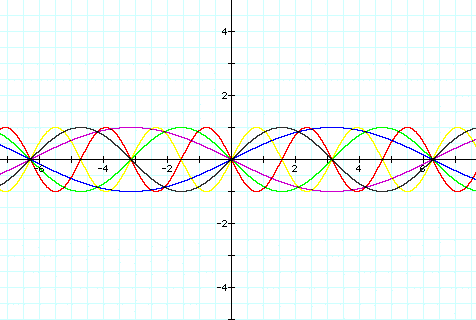
The graph corresponds to the following functions:

Look at the following two function on the graph, y=sin (2x) and y=sin ((-2)x). Their frequencies are two, and they are reflections of each other. When b=1/2 or b=-1/2, the frequency is only one-half and again there is a reflection. From observing these graphs, we can see that the frequency is the absolute value of b. We also see that when b<0, the function is reflected, or flipped.

It looks like it is shifting across the x-axis. Let's look at several on the same plane. The graph corresponds the the following equations: y=sin x; y=sin (x+(-1)); y= sin(x+1)

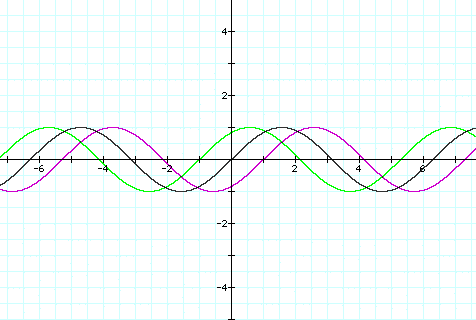
We see that when c is a positive value the original function moves to the left and when c is a negative value the original function moves to the right, along the x-axis. We can also see the distance that the function is moving directly corresponds to the c value.

We know that if a or b are negative, then the function is reflected. What if a and b are both negative?

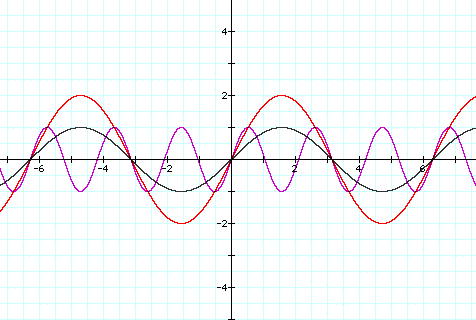
We see that the functions do not reflect. When both a and b are negative, they cancel each other. We could also consider this as a double reflection, which would look like the graph when a and b are positive.

Now, we have seen the effects of a, b, and c. By looking at the different graphs, we saw that a determines the altitude, b determines the frequency, and c determines the shift (distance and direction) along the x-axis. We have also seen when one of the values a or b is negative, the graph looks like a reflection of when a and b are positive. However, if a and b are both negative it gives no reflection.

Return