
Parametric Equations
By: Kimberly Young and Mindy Swain
Consider the following parametric equation:
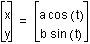 , where
, where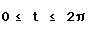
We have seen from prior investigations that
different values of coefficients can an effect of the graphs of
the functions. It is the same for parametric equations. Let's
investigate and determine what effects a and b have on the above
equation.
First consider when a=b. I began by graphing
the equation when a=b=1, a=b=2, and a=b=-2. (As shown below. The colors correspond to the graph.
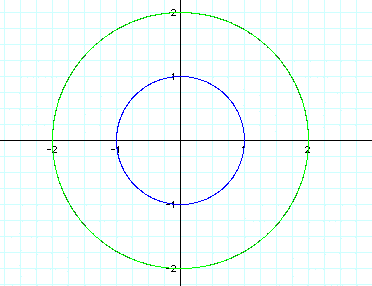
From looking at the graph, I noticed two things:
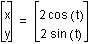 and
and 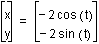 are the same graph. This
is why we cannot see the red graph. We can generalize that when
a=b, positive values for a and b generate the same graph as negative
values.
are the same graph. This
is why we cannot see the red graph. We can generalize that when
a=b, positive values for a and b generate the same graph as negative
values.
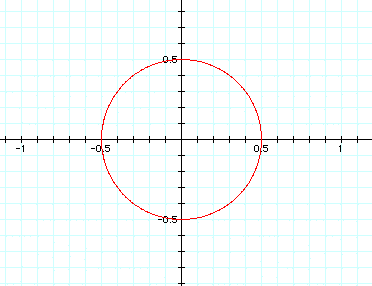
When a=b, it determines the radius of the
circle that corresponds to the graph. For example if I had 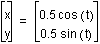 ,
I would expect to see a graph of a circle with radius 0.5, as
seen below:
,
I would expect to see a graph of a circle with radius 0.5, as
seen below:
What happens when a is not equal to b?
Consider the following equations:
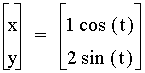 ,
, 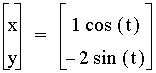 ,
, 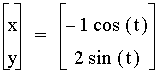 , and
, and 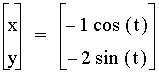 .
.
The following graph is the graph for all
four equations.
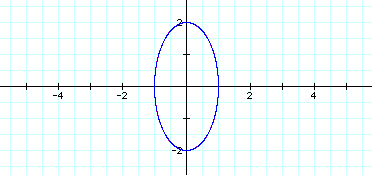
The |a| is the distance from the origin on
the x-axis and the |b| is the distance from the origin on the
y-axis.



and
are the same graph. This is why we cannot see the red graph. We can generalize that when a=b, positive values for a and b generate the same graph as negative values.
, I would expect to see a graph of a circle with radius 0.5, as seen below:
,
,
, and
.