
Investigating
Orthocenters of Triangles
By: Kimberly Young
An orthocenter of a triangle
is the common intersection of three lines containing the altitudes. To construct an Orthocenter of
a triangle, using GSP, begin with a triangle. Then construct the
altitude for each angle and side. In the picture below, H is Orthocenter.
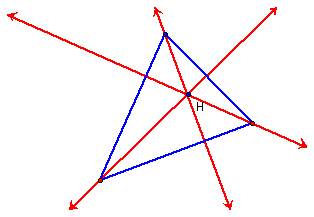
We can look at how the
Orthocenter changes as the size of the triangle varies. Click here. With the point labeled drag, explore
how the orthocenter changes as the size of the triangle changes.
Are there any conclusions you can draw?
There are several neat
things that happen when we change the size of the triangle. Lets
take a look at an obtuse, acute, and right triangle and compare
their orthocenters. In all the pictures below, H is the orthocenter.
Acute Triangle

Obtuse Triangle

Right Triangle:
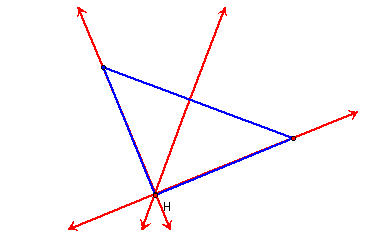
There are three distinctions
in the orthocenter of each of the triangles above. The acute triangle's
orthocenter is with in the triangle, while the obtuse triangle's
is out side of the triangle and an extension of the altitude.
The right triangle's orthocenter is on the vertex of the right
angle.
By looking at the tracing
of the orthocenter, we can see something interesting about the
orthocenter of the triangle as the size of the triangle changes.
Click
HERE. After viewing this, you may see
that the trace of the orthocenter forms a shape similar to a parabola
as the size of the triangle changes.





