Pedal Triangles
By: Kimberly Young and Mindy Swain
Investigating Pedal Triangles.
First construct a pedal triangle:
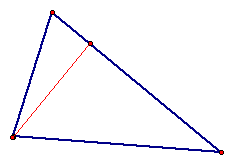
Let triangle ABC be any triangle. Then if P is any point in the
plane then the triangle formed by constructing perpendiculars
to the sides of ABC locate three points R, S, and T that are intersections.
Triangle RST is the Pedal triangle for Pedal Point P. This is
an example of a Pedal Triangle.
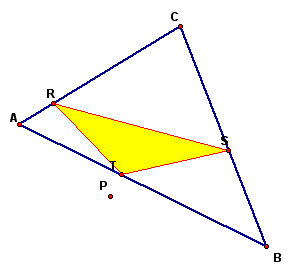
What happens to P if
P is on the side of triangle ABC?
When P is on the side of the
triangle, an image as below is constructed. Click
Here and drag the labeled point to see how the shape of the
petal triangle changes as the point changes.
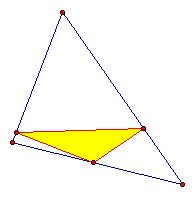
As you drag the point, you
will notice that as it approaches either vertex, the pedal triangle's
area gets smaller. It looks like the triangle will become a line
when the point is on the vertex. Change the size of the original
triangle and see if this is still true. Click
Here.
Lets take a look closer to
see what happens at the vertices.
What happens to P it
P is on the vertex of triangle ABC?
When the pedal triangle is
constructed using the vertex as the point P, a line segment is
form.