Assignment 10

Page Bird

Parametric Curves

A parametric curve in the plane is a pair of functions

where the two continuous functions define ordered pairs (x,y). The two equations are usually called the parametric equations of a curve. The extent of the curve will depend on the range of t and your work with parametric equations should pay close attention the range of t . In many applications, we think of x and y "varying with time t " or the angle of rotation that some line makes from an initial location.

Various graphing technology, such as the TI-81, TI-82, TI-83, TI-85, TI-86, TI-89, TI- 92, Ohio State Grapher, xFunction, Theorist, Graphing Calculator 3.2, and Derive, can be readily used with parametric equations. Try Graphing Calculator 3.2 or xFunction for what is probably the friendliest software.

Note: Graphing technologies compute values of (x,y) for increments of t and then construct a line segment connecting them. When the increment of t is small then these are very short segments and the curve is simulated. The TI instruments include a 'step' setting for the increments of 't' and it is possible for consecutive (x,y) to be rather far apart. This can produce interesting drawings but misrepresent the parametric curve given by the set of points. In other words, the 'step' setting is a way of drawing segments between regularly spaced but not adjacent points on the parametric curve.

EXPLORATION 8

8. Investigate

for different values of a and b. What is the curve when a < b? a = b? a > b?

Let’s start with Case 1: a<b

Let’s first try a=1 and b=4

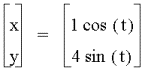
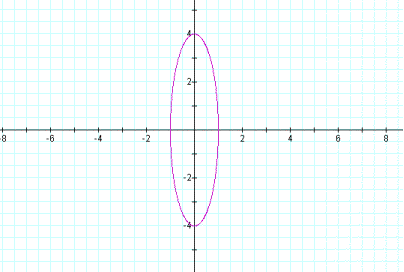
The graph is an ellipse and its major axis is vertical.

You can see that the vertices of the ellipse is (0, +4) and (0, -4).

Remember that the standard equation for an ellipse whose major axis is vertical can be found by:

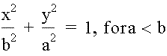
The greater the eccentricity of an ellipse, the more elongated the ellipse. Eccentricity (e) can be found by

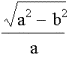
Let’s look at several different graphs with values of a and b such that a<b.

Can you tell which equations go with which of the graphs? While you’re at it, note the eccentricity of each ellipse.

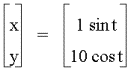
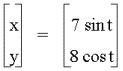
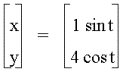
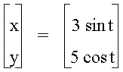
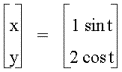
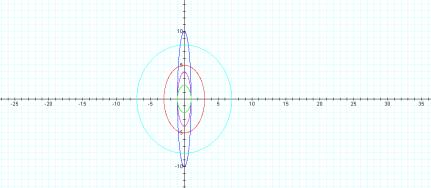
A =1, b =4

A=1, b=10

A=7, b=8

A=3, b=5

A=1, b=2

This graph shows another important property of ellipses. The maximum and minimum x values can easily be seen along the x-axis and is the same as the b values, given by (0, b) or (0, -b). So as b gets larger, the eccentricity increases.

One last observation regarding a<b. What if a and b are negative? Does the ellipse have the same characteristics?

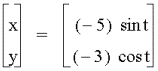
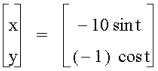
Let’s look at some more graphs to see what happens.

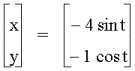
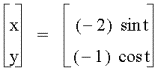
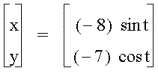
a =-1, b =-4

a=-1, b=-10

a=-7, b=-8

a=-3, b=-5

a=-1, b=-2

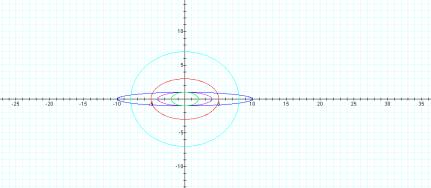
The eccentricity of the ellipses are much the same as before. However, the major axis is horizontal when the values of a and b are negative.

Notice when a=o and b=1. Our graph is a line and not an ellipse:

Before concluding case 1 let’s first look at our equations. We started out with:

We can rewrite this as

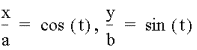
Now, if we square each side, we get:

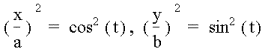
When we add each side, we get

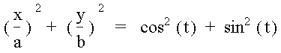
We know that

Therefore,

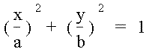
This is the standard form for an ellipse.

CASE 2: a=b

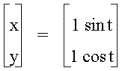
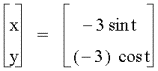
Let’s start with some graphs such that the values a=b.

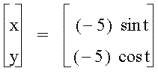
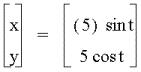
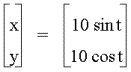
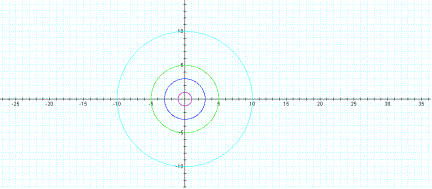
a, b = -5

a, b = 10

a, b = 5

a, b = 1

a, b = -3

Notice that each graph is a circle with the origin at (0,0) and with a radius equal to the absolute value of a and b. So why did I graph five equations, but there are only four graphs showing?

The answer is that a,b =5 and a,b =-5 graph to be the same.

Case 3: a>b

Let’s take a look using Graphing Calculator 3.2

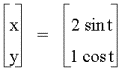
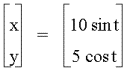
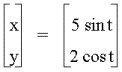
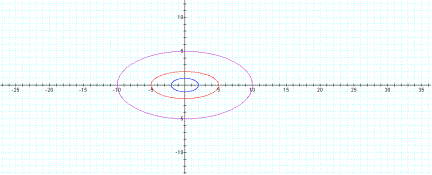
a =10, b =5

a=2, b=1

a=5, b=2

When a>b it is easy to see that the ellipses’ major axis is horizontal. The value for a determines the y maximum and minimum values.

What do you think will happen if a and b are negative values?

Investigation 2

What is changed if the equations are

where h is any real number?

Investigate with graphs for small h (e.g. -3 < h < 3).


To figure out what is going on, let’s look at some

graphs using the equations above.

Let’s first try h=-3, let a=b

a, b = 10

a, b = 4

a, b = 5

a, b = 3

The equations graphed here are:

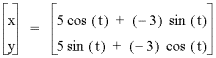
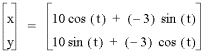
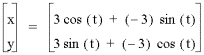
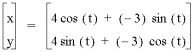
As a=b gets larger so does the graph.

So, what if we try h=-2 with the same a=b values above.

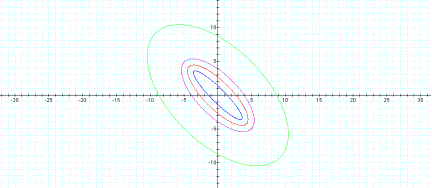
As h increases, the eccentricity decreases. Below are the graphs for h=0.

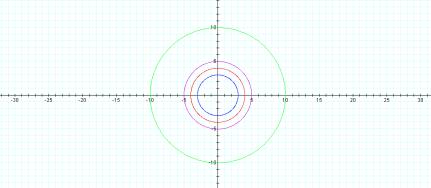
Graphing h= 1, 2, 3 the eccentricity of the ellipse corresponds with the eccentricity of h=-1, -2, and –3 respectively. However, it is a reflection of the negative values.

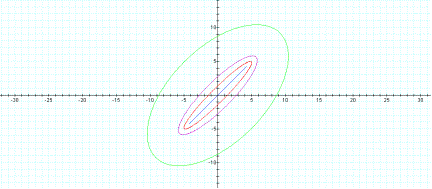
Playing around with the values of a, b, and h yields different ellipses some with more or less eccentricity then above. Click here to see a dynamic graph with different h values. You can change the a and b values as well.

Click here to return to my home page.