Assignment 7

Page Bird

Tangent Circles

Given two circles and a point on one of the circles. Construct a circle tangent to the two circles with one point of tangency being the designated point.

The goal is to first understand the construction of a tangent circle to two given circles. There are several steps, which I will highlight below using GSP.

Let’s say you start with these two circles.

There are several steps to constructing a tangent circle to these, the first of which include:

1) Construct a random line through the center of the big circle.

2) Construct a congruent circle to the smaller circle at the point at which the line crosses the big circle.

3) Connect the center of A with the top of circle C where it crosses line J

4) Construct the perpendicular bisector of the resulting segment.

5) Where the perpendicular bisector crosses line J is the center of the tangent circle.

6) The locus of this tangent line is an ellipse with the center of circle A and circle B as the foci.

To view the tangent circle for different tangent circles click here. To view the locus for different tangent circles click here.

There are other circles to consider. For example:

a) the smaller circle may be external to the tangent circle. Click here to view a GSP file of this example.

b) the smaller circle is internal to the tangent circle. Click here to view a GSP file of this example.

c) the two given circles intersect as seen below:

Click here to view a GSP file of this example.

d) the two given circles are disjoint as seen below

Click here to view a dynamic GSP clip of this.

There are several things to note regarding the locus of the tangent circles. So I will copy a picture of each case below:

When the smaller circle is internal, the locus is an eclipse. When the two circles intersect, the locus becomes thinner and longer:

As the circles become disjoint, the locus becomes a hyperbola with the foci at the centers of the given circles:

If the tangent circle is the same as one of the given circles, then the locus becomes a very thin hyperbola located at the center of the circles.

A few observations:

The further apart the given circles are when they are disjoint, the wider the hyperbolas become. As the circles get closer, the hyperbolas become thinner. As the circles become tangent and then overlap, the locus becomes an ellipse—very thin, and then as the circles overlap more and more the eccentricity becomes less. This continues as the smaller circle is on the interior of the bigger circle. If the circles have the same center, the locus is a circle.

Click here to investigate the locus more closely.

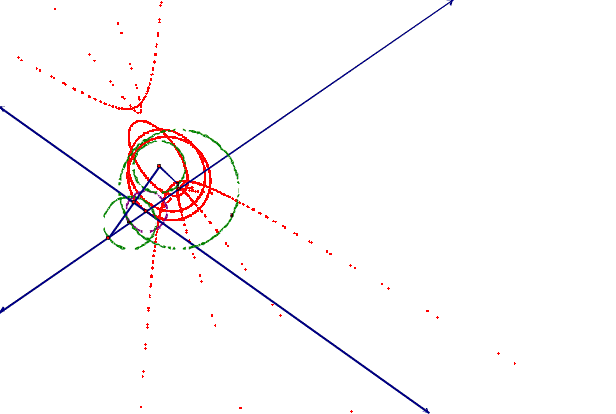
The picture above shows an overlap of the different possiblilities for the locus.

Return