Assignment 8
Page Bird
Altitudes and Orthocenters
12. Given triangle ABC. Construct the Orthocenter H. Let points D, E, and
F be the feet of the perpendiculars from A, B, and C respectfully. Prove:
![]()
![]()
Click HERE for a GSP sketch. What if ABC is an obtuse triangle?
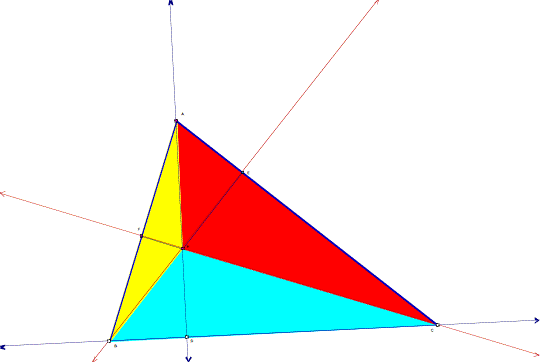
One way to approach this problem is to think of the area of triangle ABC as a sum of the area of the three triangles above which can be recognized with the three colors.

So the area of triangle ABC
can be written as:

Also, the area of triangle ABC
divided by itself is 1
There are
several ways to express the area of triangle ABC.
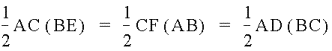
Another way
to express the area of triangle ABC divided by the area of triangle ABC
is
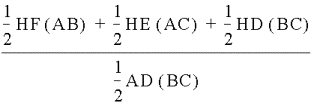
The goal is
to reduce this. The first step in
the process is
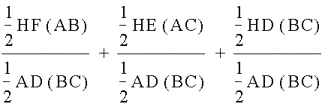
This can be
reduced to
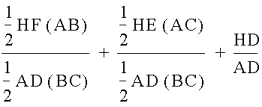
Since
1/2CF(AB) =
1/2AD(BC)
and
1/2AD(BC)
=1/2 AC(BE)
We can
substitute into the equation above.
Therefore,
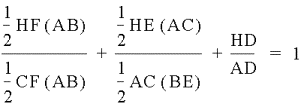
This
reduces to
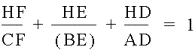
Therefore
this proves our statement through a series of substitutions and simple
geometric relationships.
Next, we
want to show that
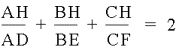
Let’s go
back to the picture:
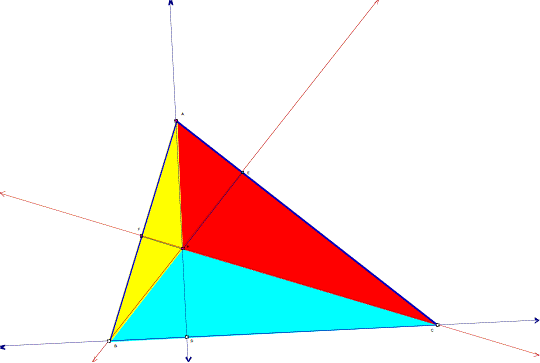
Looking at the picture above, we see
that
AH = AD –
HD
BH = BE –
HE
CH = CF –
HF
These can
be substituted into the fractions to get
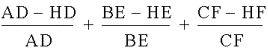
This can be
rewritten as
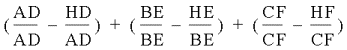
And then
reduced to
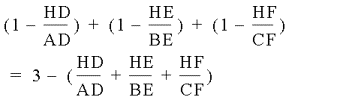
Since
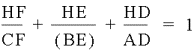
Then 3-1=2.
Therefore,
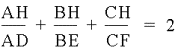
Now this brings us to the question, does this apply to obtuse triangles?

To find out, I constructed the
orthocenter for an obtuse triangle.
The orthocenter lies outside the triangle when it is obtuse.
The red
triangle represents the given obtuse triangle, and H is the orthocenter. I then found that the orthocenter of
the triangle BCH was point A.
Based on this, I measured segments HF, CF, HE, BE, HD, and AD to see if
the relationship held.
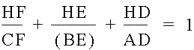
They did
not. Based on this and the fact
that the orthocenter lies outside the obtuse triangle, this relationship does
not hold for obtuse triangles.
To check
this out yourself, click here.