Page Bird
The Tortoise and the Hare
A tortoise and a hare start at the same time
in a 10-mile race. The hare runs for 20 minutes at 12 mph; stops
to rest; falls asleep for several minutes; awakes; and finishes
the race, again running at 12 mph. Meanwhile, the tortoise plugs
along at the same constant rate of 2 mph throughout the race.
What is the least amount of time the hare was asleep if the tortoise
wins the race?
I started by plotting the tortoise's
rate since he travels a constant rate.
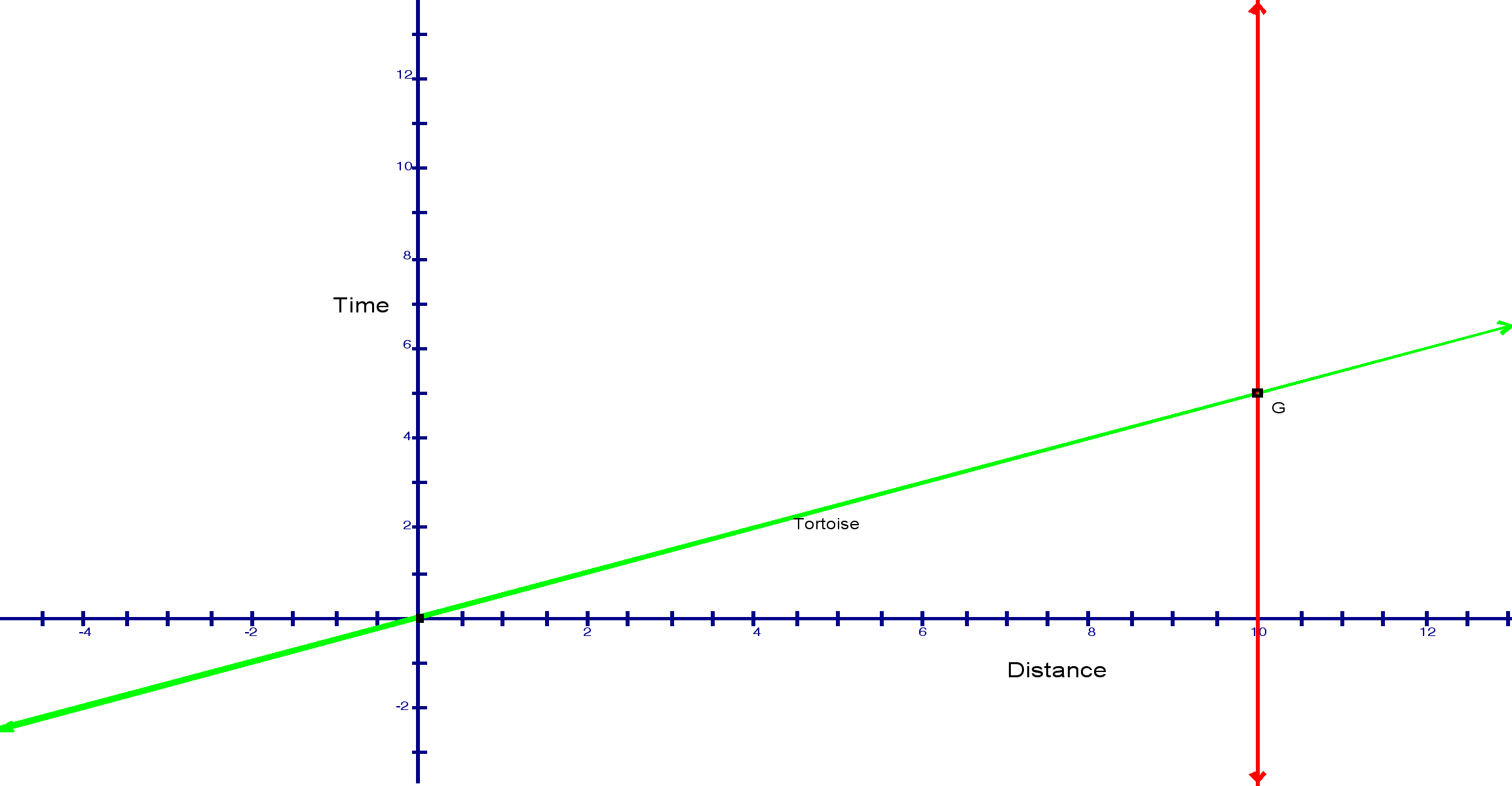
The red line is the finish line at 10 miles.
We can see that the tortoise will finish in five hours.
The hare on the other hand runs at
12 mph for only 20 minutes. Using the dilation and translation
function on GSP I created a segment that represented this rate.
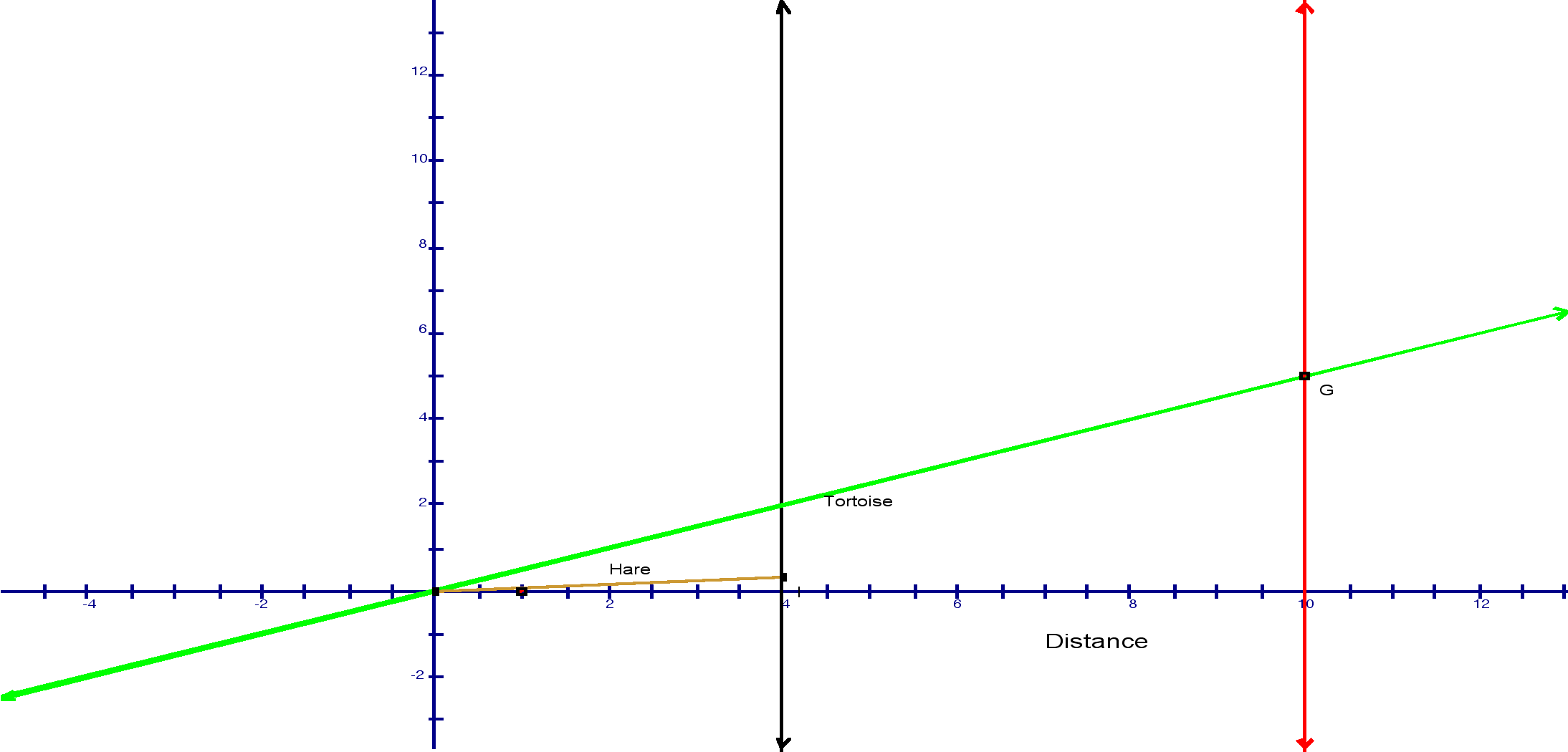
At this point, time is ticking away, but the
hare is napping so all that needed to be done was to play around
with the minimum amount of time he could nap if he is to lose.
Using GSP, I changed the origin to be a floating y-value and x
to be stationary at four miles.
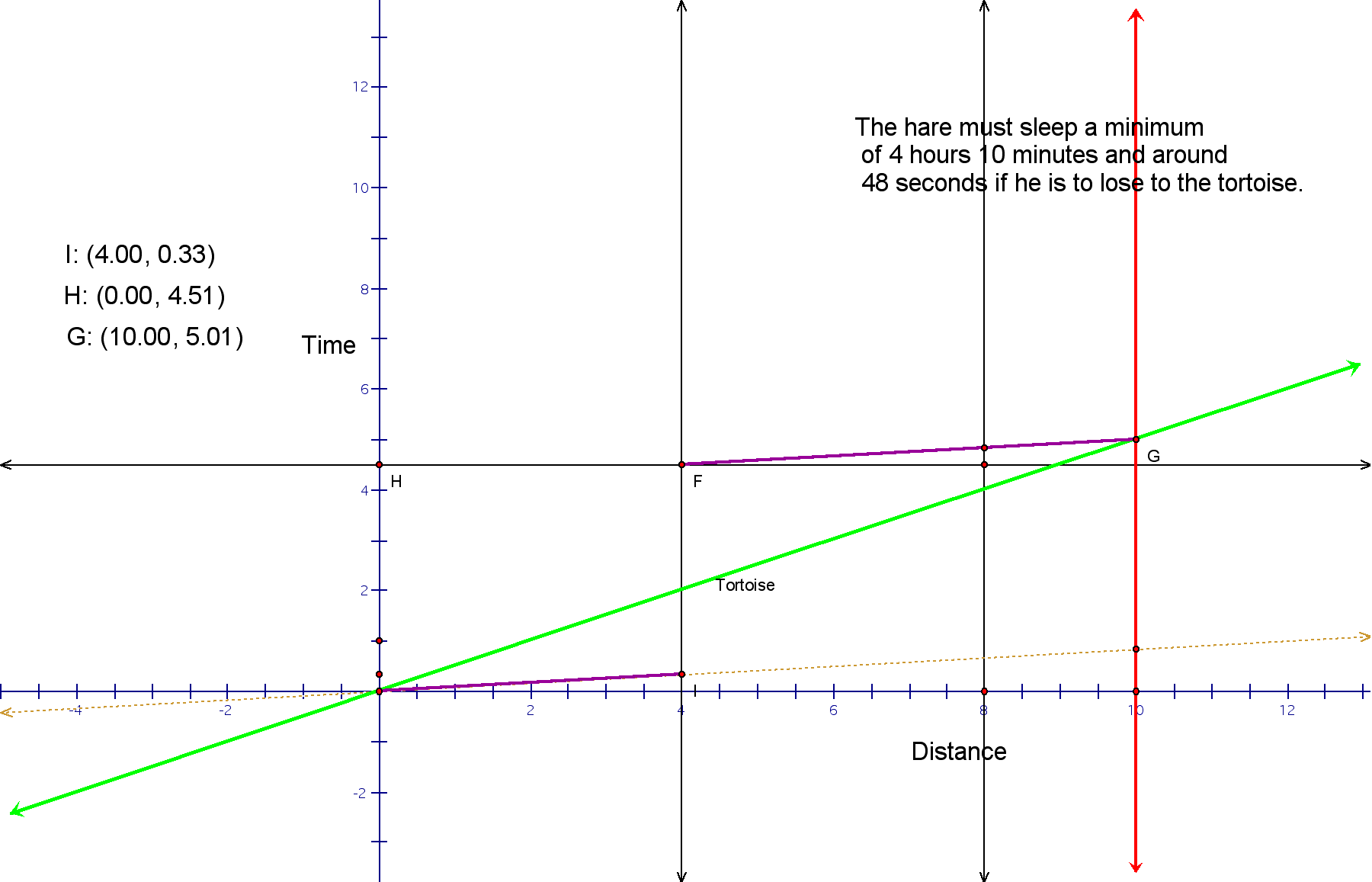
Looking at the graph, we can see that
if the hare wakes at 4.51 or about 4 hours and 30 minutes, then
it will finish at exactly the same time as the tortoise. If the
hare finishes at the same time as the tortoise, then the hare
would have napped 4.51-0.33 = 4.18 hours or 4 hours 10 minutes
and about 48 seconds. So if the hare sleeps longer than this then
he will lose the race.
Another way to say this is the minimum amount of time the hare
can sleep and lose the race is 4 hours 10 minutes and 49 seconds.
Click here
to see a GSP file.
Return to my EMAT
6690 page.