Complete a Write-up on your Web Page for the following investigation. This should be individual work.
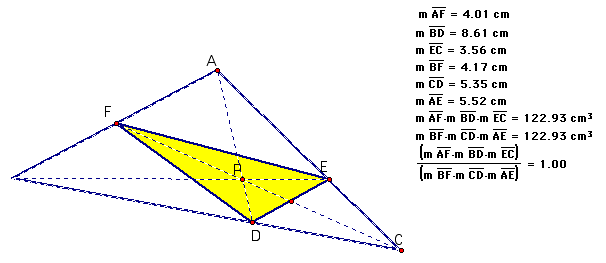
A. Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.
Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.
Below are some of my explorations.
When P is inside the triangle:

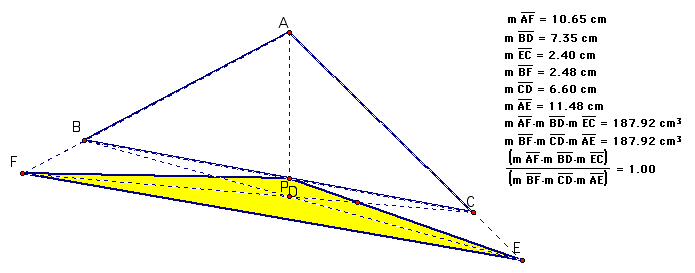
When P is outside the triangle:
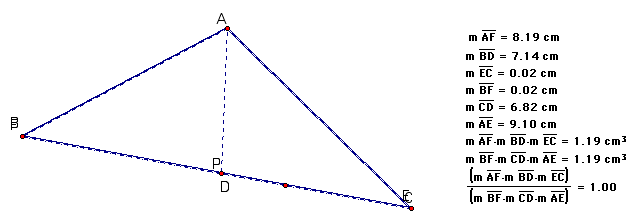
When P lies on a side of triangle ABC.
The GSP sketches here are pretty convincing
that 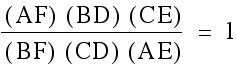 .
.
But the question is how do we prove this. Which brings us to part B of this assignment.
Click here to see a dynamic GSP sketch.
B. Conjecture?
Prove it! (you may need draw some parallel lines to produce
some similar triangles) Can the result be generalized (using lines
rather than segments to construct ABC) so that point P can be
outside the triangle? Show a working GSP sketch.
Using the parallel lines below, let's look at a proof.
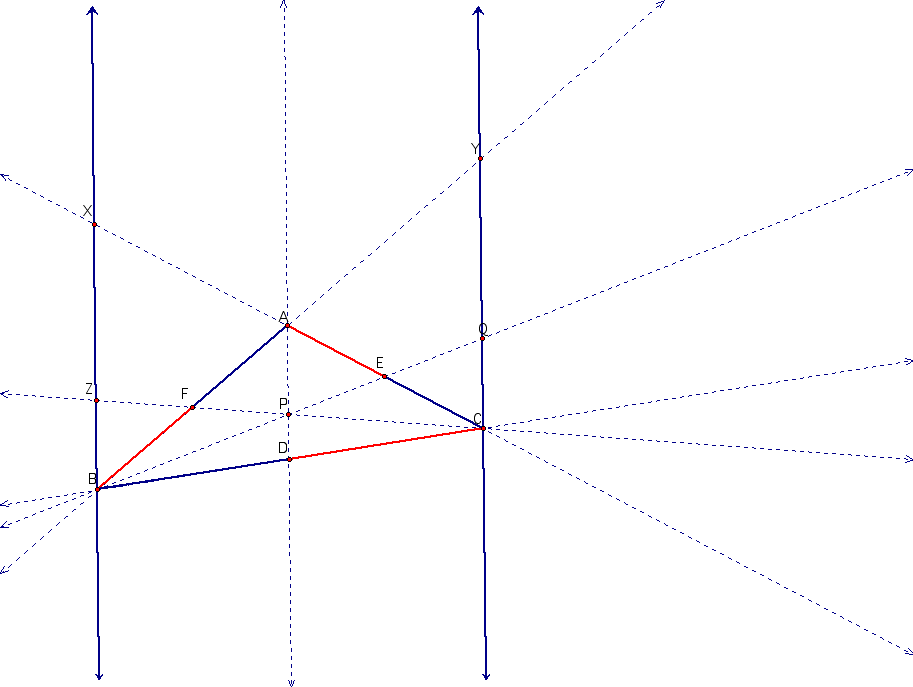
By similar triangles 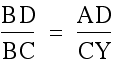 and
and 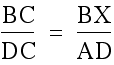 .
.
We can also make the relationship, 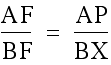 and
and 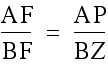 by vertical angles.
by vertical angles.
When we multiply these relationships, we get
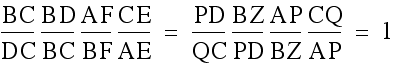 .
.
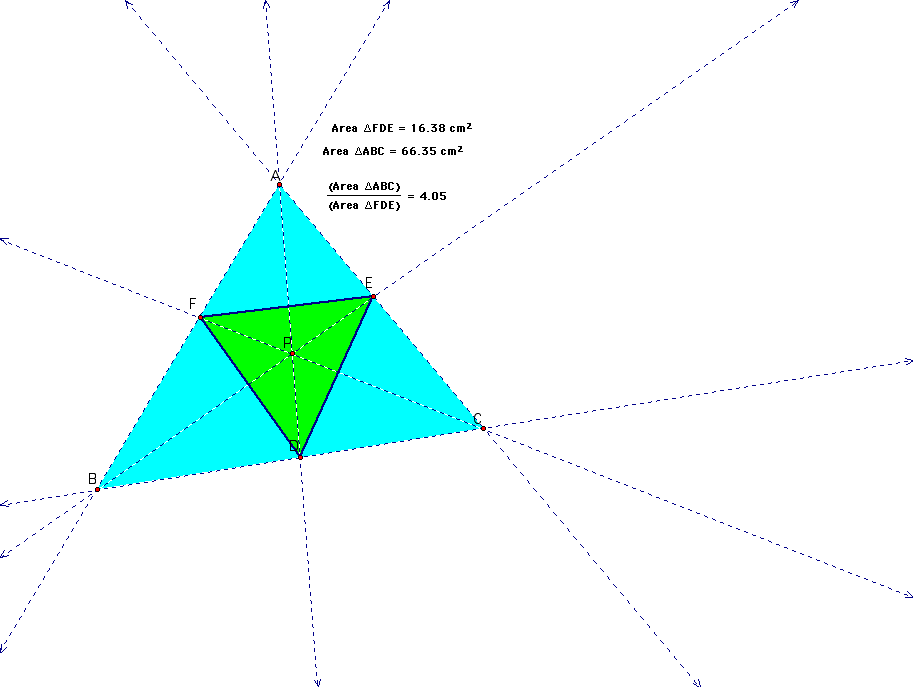
C. Show that
when P is inside triangle ABC, the ratio of the areas of triangle
ABC and triangle DEF is always greater than or equal to 4. When
is it equal to 4?
Here is one example I looked at. In each example, the ratio was
always greater than or equal to 4. I found one example when the
ratio was equal to four. Thei occurs when triangle DEF has its
vertices at the midpoints of the sides of the triangle. Click
here to see a GSP dynamic sketch.