

Statement of problem:
Find 2 linear functions g(x) and f(x) such that their product
h(x) = g(x) f(x)
is tangent to both g(x) and h(x) at two distinct points.
The product of two linear functions ![]()
will be a quadratic equation of the form ![]() .
.
My first step was to take a "guess" and graph the equations. I pictured the h(x) being a parabola with the g(x) and f(x) lines crossing (one with positive slope, one with negative slope).
I used ![]() and
and ![]() :
:
Obviously neither line is tangent. It appears that moving either line (or both) such that the y value of their intersection moves up will get us closer.
So I tryed graphing these two lines, moving the y intercepts up (I simply changed the b values from 3 to 5):
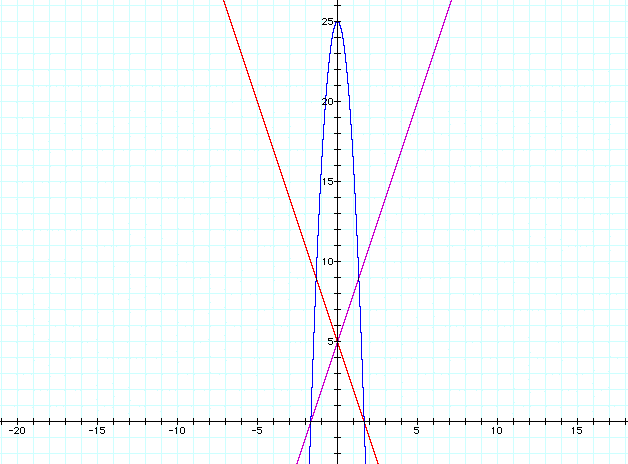
That made it worse! While the intersection of the lines moved up, the "y" value of the vertex of the parabola went from 9 to 25.
What if I move just one line? Try our y=3x+3, and change the second equation to
y=-3x - 2. The composite function is ![]() , or
, or ![]()
Our graph is as follows:
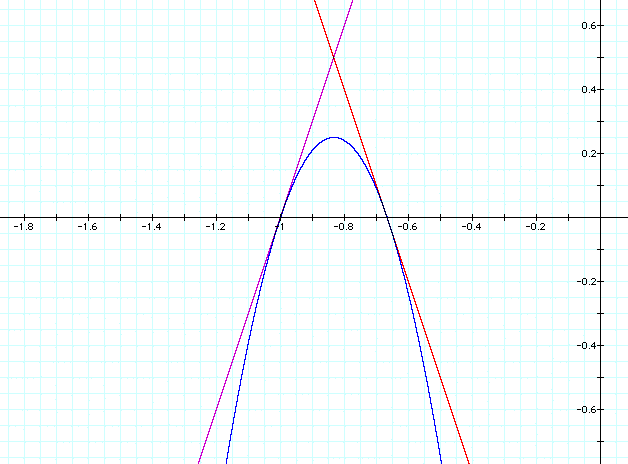
That looks like it works! Was I that lucky? Setting our first linear equation equal to the composite, we have 3x + 3 = (3x + 3)(-3x -2). This has only one solution at x=-1, so that is tangent. Likewise -3x - 2 = (3x + 3)(-3x -2) has just one solution, at x = -2/3. Great!
But why did that work? And can we find others?
Let's try making the slopes of the lines 1 and -1 instead of 3 and -3. I have shown both graphs together below:
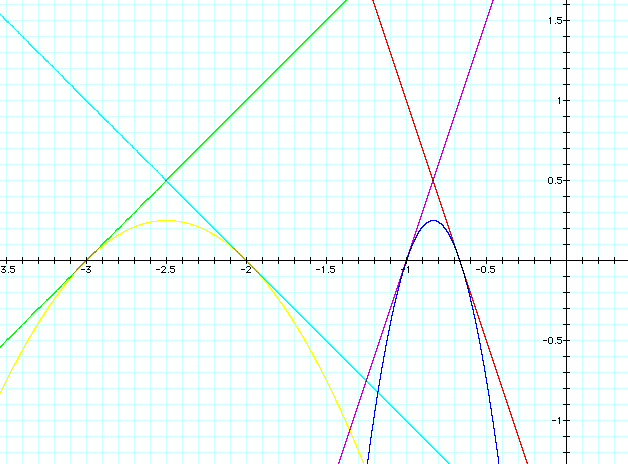
Here is yet another added, with slopes of 7 and -7. Notice that the intersection of the lines appear to have the same value of y for each pair. I have shown a line at y = .5 to illustrate this.
Likewise, the vertices of the parabolas are all at y = .25, and I have shown a line.
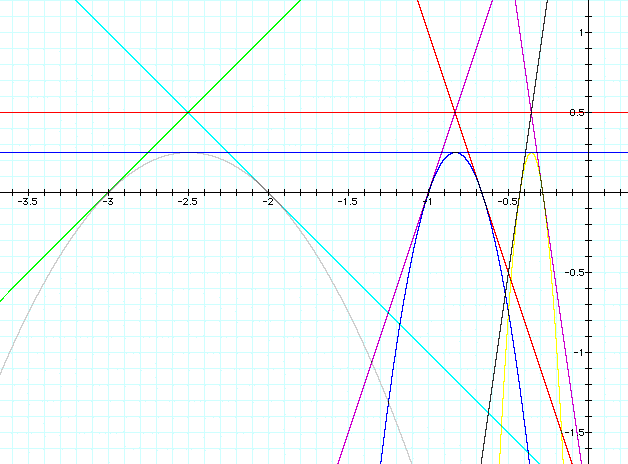
So how can we choose 2 lines that will create this effect without just guessing? From our observation, it appears that if the lines have slopes that are "negative of each other" and they intersect at y = .5 they should work.
Lets try that with an arbitrary line of y = 4x - 1.
At y = .5 we have
.5 = 4x - 1
or x = 3/8
So our "companion" line should be y = -4x + b, with y=.5 when x=3/8.
So again at y = .5, with x = 3/8,
.5 = -4 (3/8) + b, or
b = 2.
So our other line must be y = -4x + 2. Lets try it!
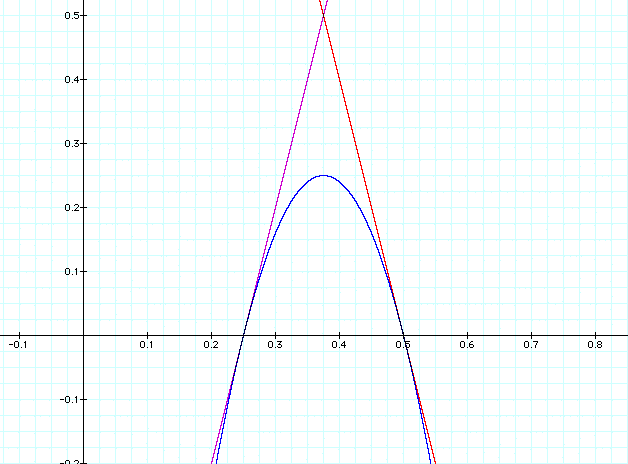
So, without proof, we have observed that the product of two linear functions is tangent to each of the two functions when the linear functions are of the form y = mx + b and
y = -mx +c with intersection at y=.5.