Let us consider the equation 
.
When a, b and k all equal 1 we have:
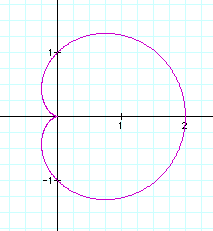
Change a, b and k to 2 and we get:
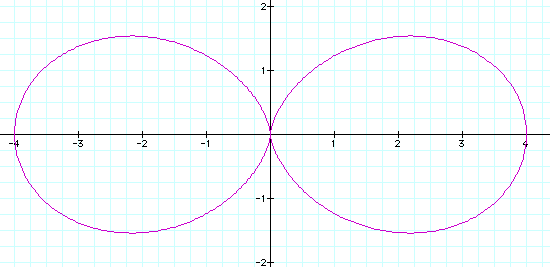
When we set them all equal to 3 we get:
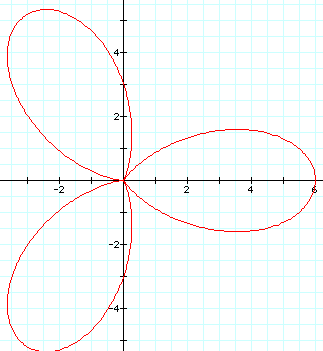
Lets try 4 and 5, and I think we'll have a pattern!
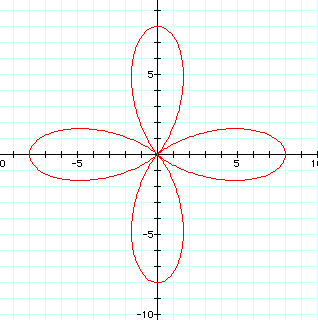
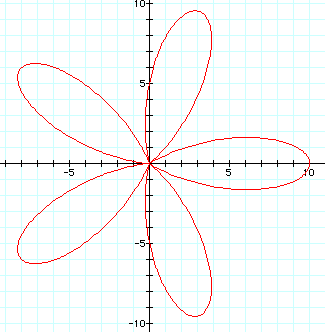
So, the number of leaves is equal to the integer value of a, b, and k when they're all equal.
But look at this. Leaving a = 5 and b = 5, with k = 2, we have 2 leaves. Maybe k is the key here with regard to the number of leaves we have.
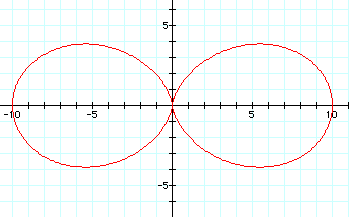
Here we have a and b both equal to 6.2, with k = 7. Seven leaves!
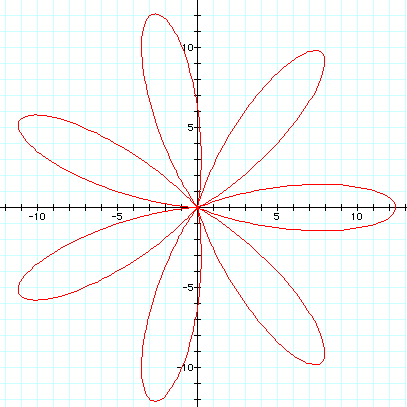
Now compare that (still in red) to 
(in blue).
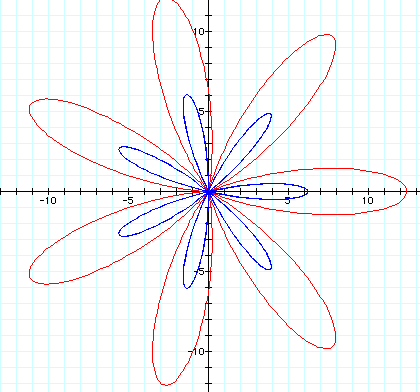
But look what happens when we make k an even number, like 4.
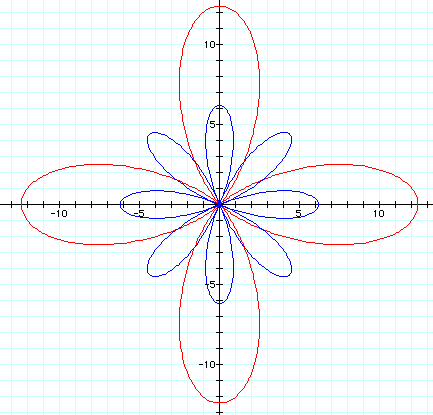
So, when k is even it appears we have twice as many leaves with the second equation, while there are the same amount when k is odd.
Here I simply changed cosine to sine in both equations.
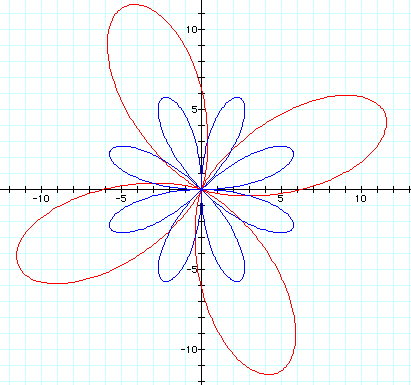
That looks a lot like the prior graph, just rotated a little bit about the origin.