Lets look at the graph of some quadratic equations.
These are equations that are of the form y=
.
Arbitrarily, lets set a=1 and c=1. We can then examine 
for various values of b.
Lets look at a movie first. Here is the parabola
formed by the equation, with b varying from 5 (the parabola is
"lower left" at that point) to -5 (where the parabola
is "lower right"). When b=0, the parabola is at "top
dead center" (to borrow an automotive engine term) - a parabola
with equation 
, vertex
at (0,1).
Here is a still picture with b=5, 3, 1, 0, -1, -3, -5 as vertex moves left to right:
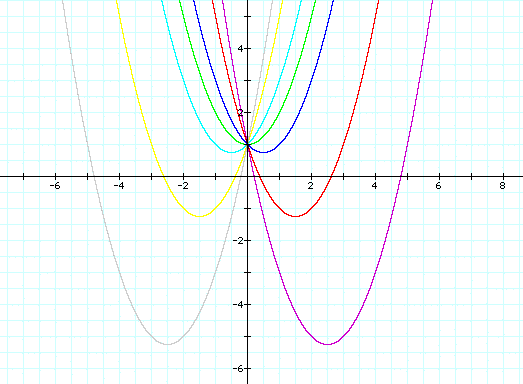
Look at the vertices of each parabola. What if we were to graph the locus of points formed by the vertices? What would it look like? How would we define it (ie, what is the equation of that locus of points?)
Well, the vertex in each of the parabolas occurs
where y has a minimum value. Taking the derivative, we have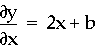 
. Since this must equal 0 at the minimum,
we have x = -b/2. So the vertex of each parabola occurs when x
= -b/2. Let's graph that line for b = 5,4,...,-4,-5.
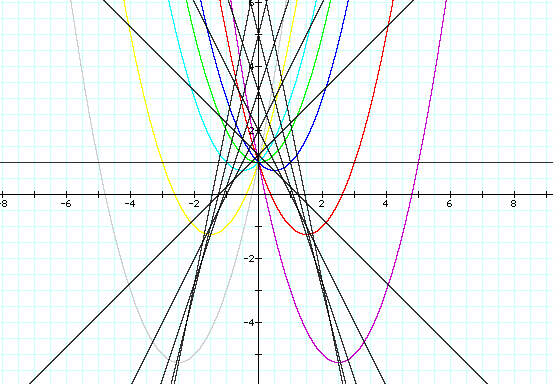
Since each vertex, or minimum, occurs at x=-b/2, then we can define the locus of vertex points by substituting -b/2 for x in our original parabola equation:
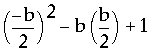
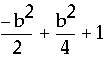
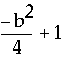
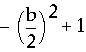
Finally,
.
When we graph this, we see that indeed it does go through each vertex!
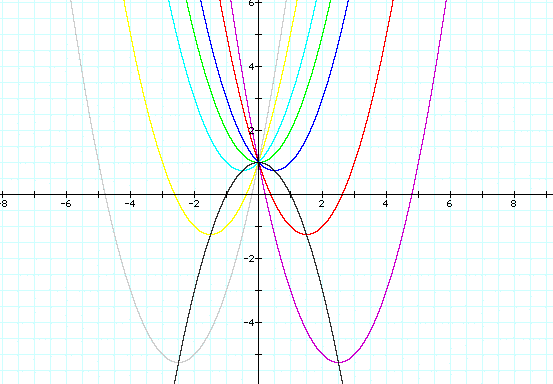
So, the equation that defines the locust of
points formed by the vertices of the parabolas defined by is .