

Here is a fun exploration using GSP.
The problem is as follows. At what yard line does a college football kicker have the optimal angle to kick a field goal from the hashmarks?
A bit of knowledge regarding field dimensions is needed. They can be found here.
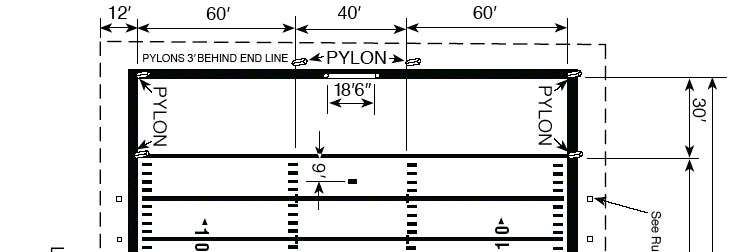
A simple GSP file was created to create a picture" of the field. The first step was to use the "Graph" "Show Grid" commands, showing a cartesian plane. The "field" was constructed in Quadrant I and IV.
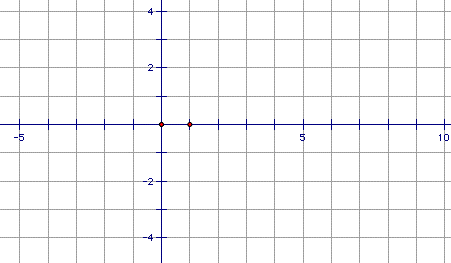
Using the coordinate plane "unit" as a yard allows us to use the "Measure" "Coordinate Distance" command to measure yardage.
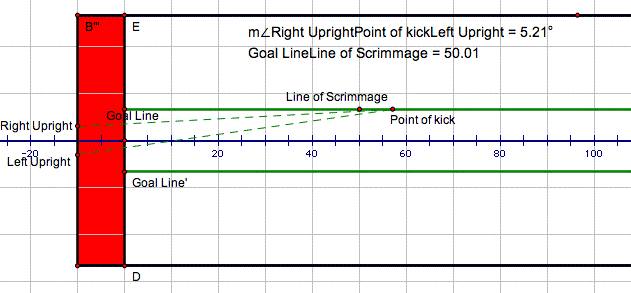
By dragging the Line of Scrimmage point along the hash mark we can watch the angle measurement change. Position the line of scrimmage for the maximum angle and we have the optimal kicking distance. You can click here to open the GSP file (you'll need the software on your computer) and try it yourself! Just drag the line of scrimmage point and watch the angle measurement.
Would it ever make sense to take a five yard penalty in an effort to increase the angle?
It appears from my GSP file that "the closer the better". Is this what you expected? Not me! In fact, I am concerned that I have made an error, but cannot see it. What do you think? Can you find a mistake?