Construct any triangle ABC:

Construct the orthocenter, H, of triangle ABC. The orthocenter is the common intersection of the altitudes, the segments from the vertices perpendicular to the opposite sides.

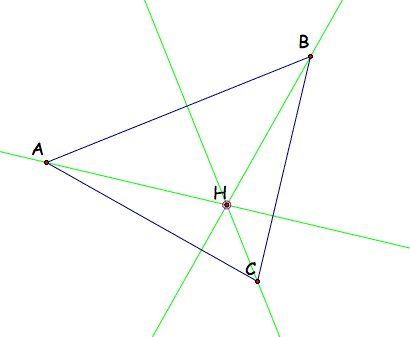
Now consider triangles HBC, HAB, and HAC.

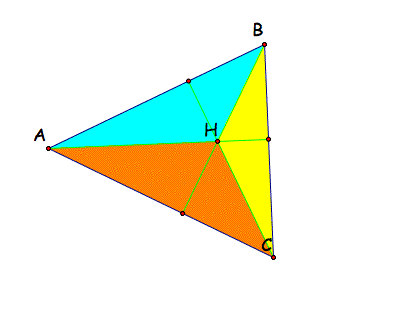
Now A is the orthocenter of trinagle HBC, B is the orthocenter of triangle HAC, and C is the orthocenter of triangle HAB.

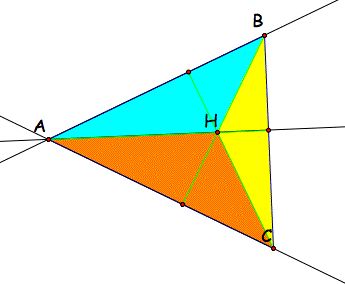
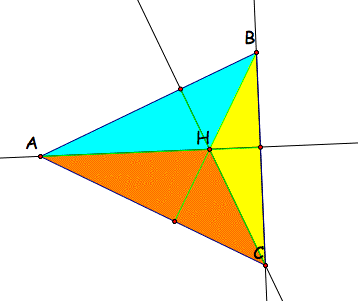
So, the orthocenters of the three triangles created using the orthocenter of triangle ABC are the original vertices, A, B, and C!

Now, add the circumcircles of each of the four triangles.

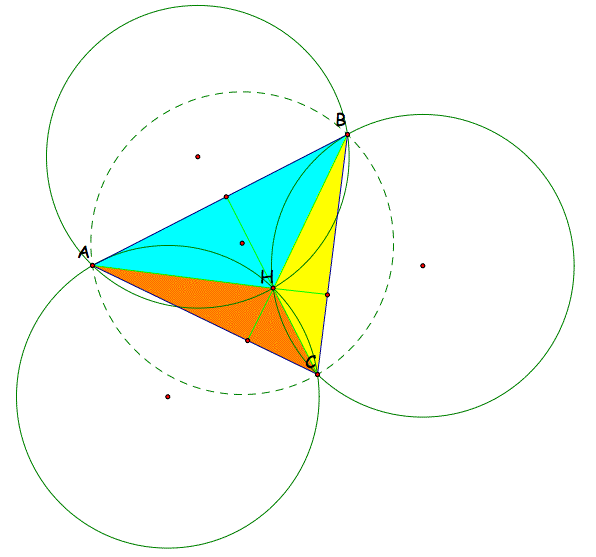
You can click here to open the Geometer's Sketchpad file (of course, you'll need the software on your computer). Try moving the vertices around and see what you come up with.

It appears that all four circles share the same radius. It also looks like they all intersect the origninal orthocenter, H. What else can you find?

Return