

This is a brief introduction to Pedal Triangles. We will construct one using GSP, then provide a "live" version for you to explore!
Consider triangle ABC and any point P in the plane.
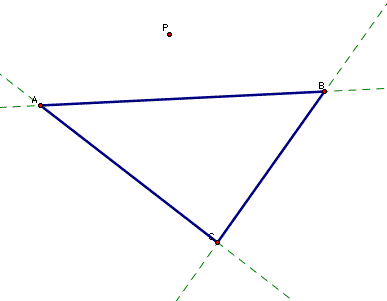
Construct the perpendicular from P to each side (or extended side) of the triangle.
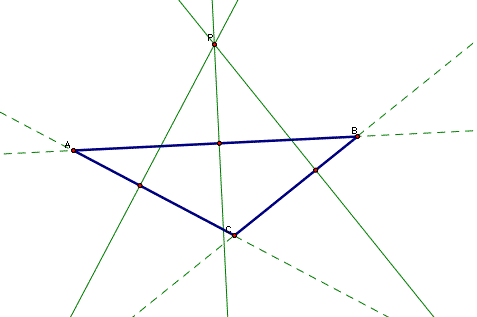
The 3 points at which the perpendiculars intersect the "sides" form the vertices of a triangle we call the Pedal Triangle. P is known as the Pedal Point.
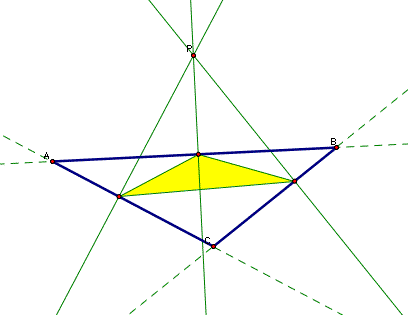
So there it is, in yellow, our Pedal Triangle.
GSP provides an excellent vehicle to investigate what happens to the Pedal Triangle as we move the Pedal Point around. Lets go ahead and add some points representing the centers of our original triangle ABC. I'll show a picture, then provide a GSP file that you can manipulate yourself.
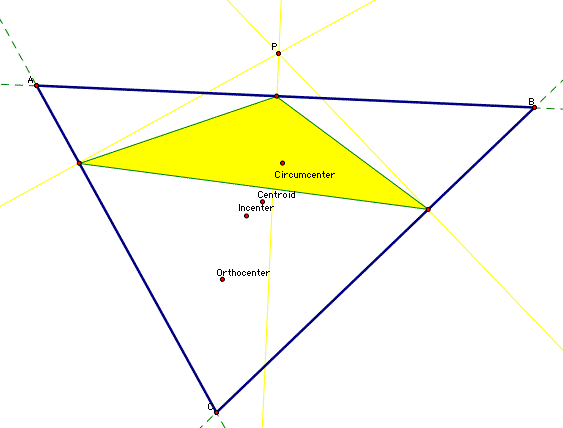
I have added the Circumcenter, Centroid, Incenter, and Orthocenter to the picture above. Go ahead and click here to manipulate P to match up with the various centers and vertices of triangle ABC (you'll need a copy of GSP on your computer).