The spreadsheet is a utility tool that can be adapted to many different explorations, presentations, and simulations in mathematics. There are spreadsheets available on almost any platform. An essential feature should be the ability to make graphs and charts from the matrix of data.

Compounding interest is "interest on interest." It is a method of calculating interest where the interest is added to the original principle. This new value is now our principle for the next time period. In this method the interest earned in past terms can earn interest in future terms. Simple interest is a type of interest that is payed only on the original amount deposited and not on past interest payed.

Let's look at an example of what can happen to a savings account when one is computed using compound interest verses one that is payed using simple interest.

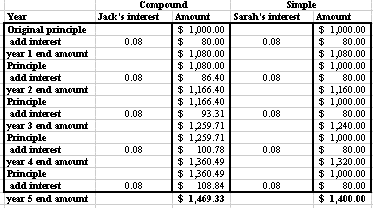
Jack and Sarah both open savings accounts with a starting balance of $1000.00 on the same day. Jack's bank is paying him using compounded interest, but Sarah's bank is paying her using simple interest. Both Jack and Sarah are receiving an interest rate of 8% annually. Who do you think will have the larger balance in five years?

Both simple interest and compounded interest can be computed using formulas.

I= total interest

p= principle

r= interest rate (in decimal form)

t = time in years

Sarah started her account with $1000.00 at a rate of 8%. We looked at the total after 5 years.

I=($1000.00)(0.08)(5)

I=$400.00

S= future value

P=original principle

r= interest rate (in decimal form)

n= number of times per year the interest is compounded

t= number of years invested

Jack started his account with $1000.00 at a rate of 8%. It was compounded once a year, and we watched his account over a five year period.

S=($1000.00)(1+0.08/1)^(1)(5)

S=($1000.00)(1+0.08)^(5)

S=$1469.33

The rule of 72 is used to figure out when your money will double. If you divide 72 by the interest rate you are earning (or paying) the answer will give you the number of years until your money doubles. This rule only works on interest that is compounded once a year.

If we divided 72 by the interest rate that Jack is receiving we should be able to find out when his money will double.

72/8 = 9

Let's use our spread sheet to see if this works.

  

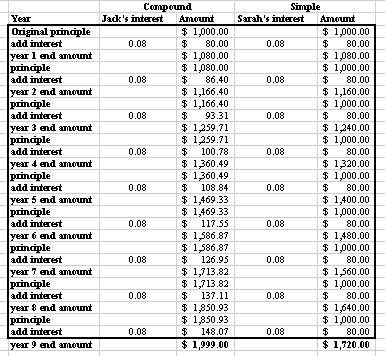
Notice that Jack's principle did double after 9 years, but look at Sarah's ending amount after 9 years. She is almost $300.00 behind Jack. So, after our investigation, would you rather earn compounded interest or simple interest? Would you rather pay compounded interest or simple interest?

We can also use excel spreadsheets to graph our information. Look at the different types of graphs that excel can generate.

Here is a simple xy graph. Notice that excel has plotted the balances after each year. We can easily see that Jack started with $1000.00 and ended year 9 with $2000.00.

 

Here is another type of graph construced by excel. This is a bar graph. From this graph we can also see Jack's beginning balance as well as his ending balance.

Return to Home Page