

Given two circles and a point on one
of the circles. Construct a circle tangent to the two circles
with one point of tangency being the designated point.
First, I will begin with two circles.
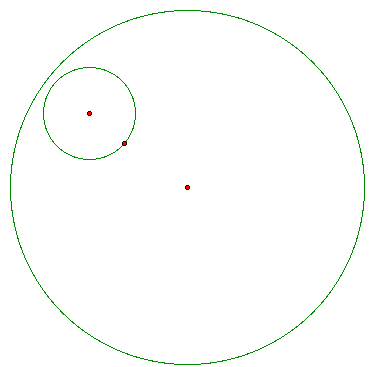
Next I will choose a point on the outer circle and construct the line that passes through that point and the center of the circle.

Next, I will find the radius of the smaller circle and use that segment to form a circle of the same radius around my point. That point will now become the center of my new circle.
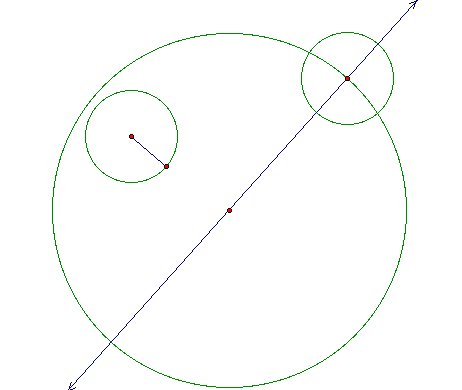
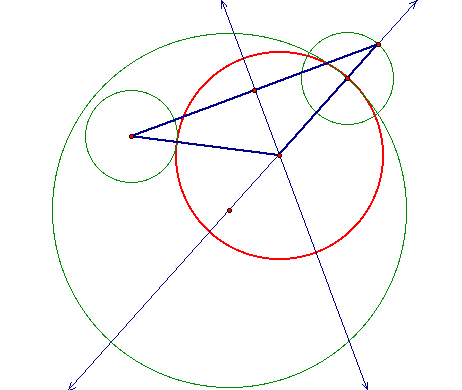
I will now construct a line from the center of the first circle to the top of the second circle. From there I will find the midpoint of the line just constructed. I then construct the perpendicular to that line through the midpoint. This new line crosses my orginal line at a point that has been marked.
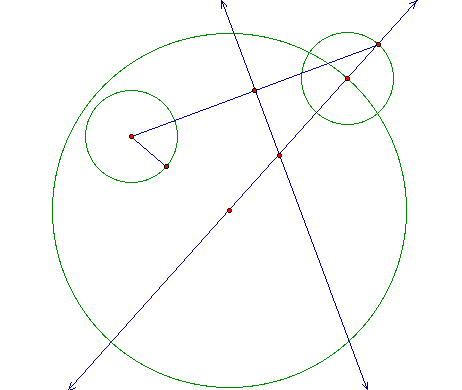
Now using this new point at the intersection of the two lines as the center of the circle I want to construct. The radius of the new circle is equal to the length of the segement from the point of intersection to the center of the last circle constructed.
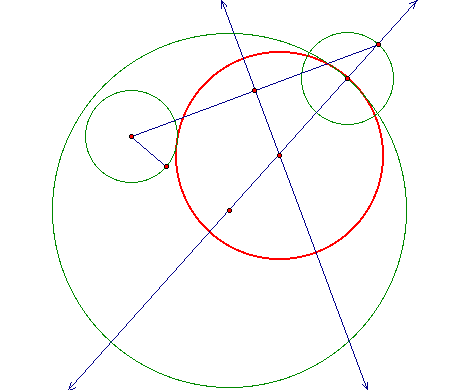
Now that I have done the construction, I will investigate the locus of the tangent circle. With GSP, I have traced the locus of the tangent circle while my arbitrary point moves around the large circle.

The blue
circle is the traced line of the movement of the locus. It appear
to be an ellipse. Notice that the perpendicular line it tangent
to the ellipse. As it moves around it will always be tangent to
the ellipse no matter where it is located.
Return to Home Page