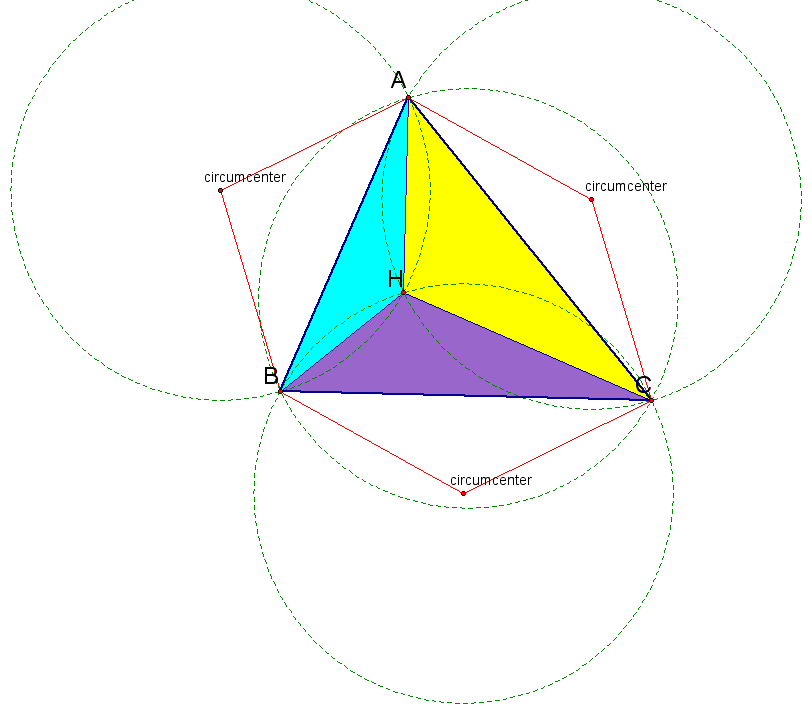
1. Construct any triangle ABC.

2. Construct the Orthocenter H of triangle ABC.

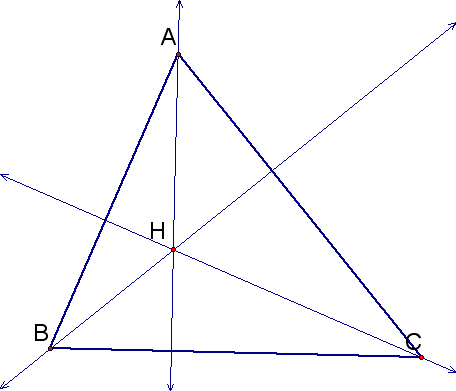
3. Construct the Orthocenter of triangle HBC.

4. Construct the Orthocenter of triangle HAB.

5. Construct the Orthocenter of triangle HAC.

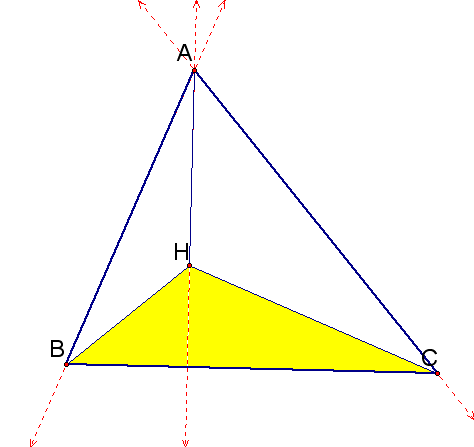
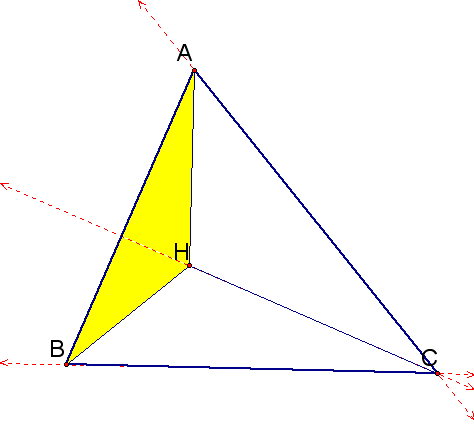
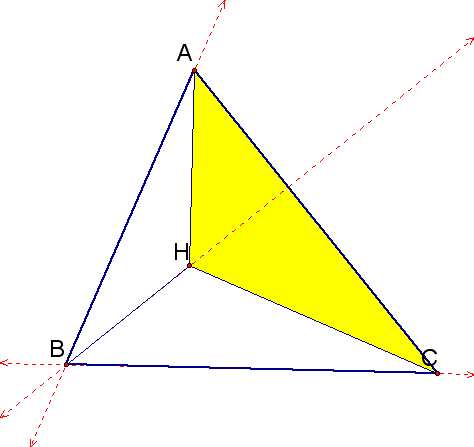
It looks like the orthocenter of our new triangle (when H is a point on the triangle) is always a vertex of the orginal triangle. How do we prove this, and does it work for any triangle?

We can see from the above diagrams that segment AC is perpendicular to segment BH, segment AB is perpendicular to segment CH, and segment BC is perpendicular to segment AH. So the orthocenter of HBC must lie on AH, AB, and AC. Therefore, the intersection of these three lines is the orthocenter, A.

A similar proof follows for HAB and HAC.

6. Construct the Circumcircles of triangles ABC, HBC, HAB, and HAC.

Return to Home Page