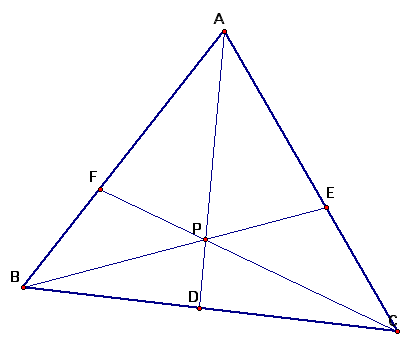
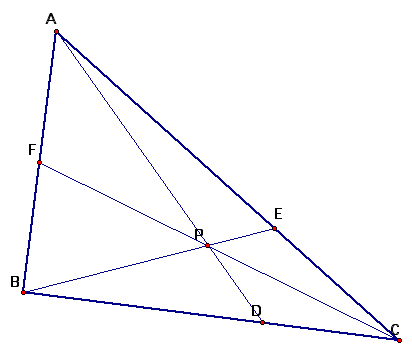
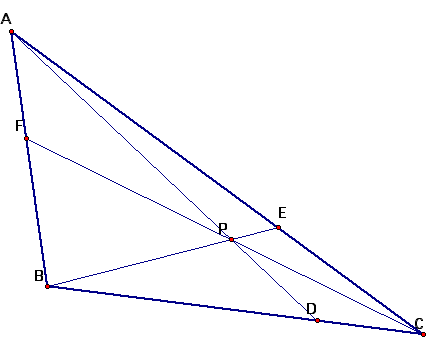
A. Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.

Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.

1.

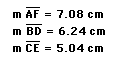
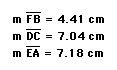
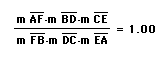
2.

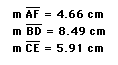
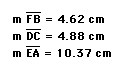
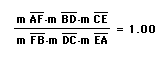
3.

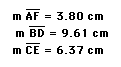
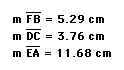
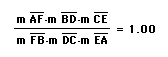
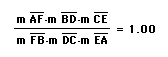
Let's prove it!!

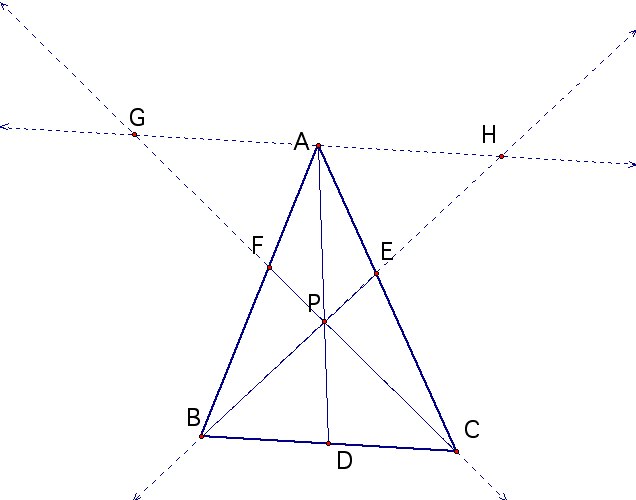
Construct a line through point A that is parallel to line BC. Extend the lines BE and CF beyond the triangle until they meet GH.

We have similar triangles

AHE and BCE

AFG and BCF

AGP and CDP

BDP and AHP

By the fact of similar triangles, we get the following ratios:

1. AE/EC = AH/CB

2. BF/FA = BC/AG

3. AG/CD = AP/DP

4. AH/BD = AP/DP

Notice that:

AG/CD = AP/ DP = AH/ BD

so,

BD/CD = AG/AH

Now multiply or ratios;

(AE/EC) (BD/CD) (BF/FA) = (AH/CB) (AG/AH) (BC/AG) = 1

We can now look to see if this holds true when P is outside of the triangle.

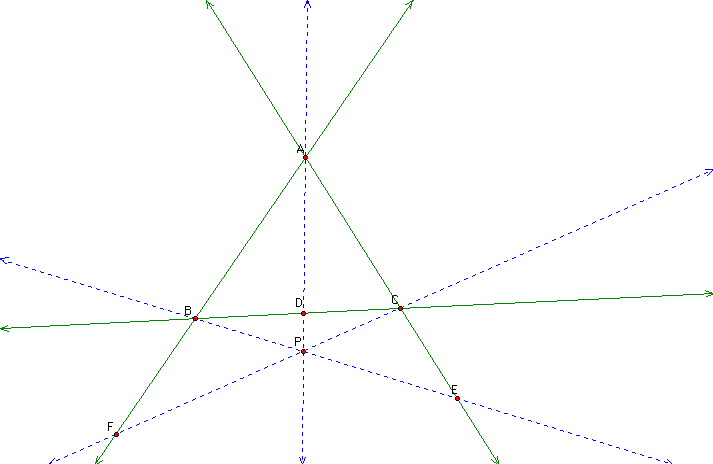
This time we would draw a line passing through points F and E that is parallel to line BC. By using the similar triangles we would find that the same ratio hold true for this as well.

Show that when P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. When is it equal to 4?

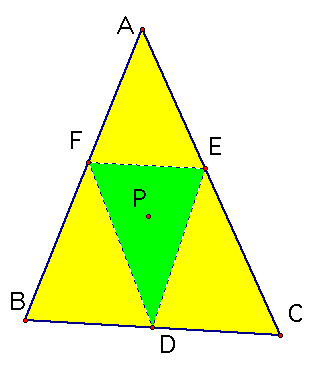
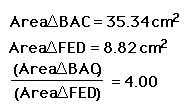
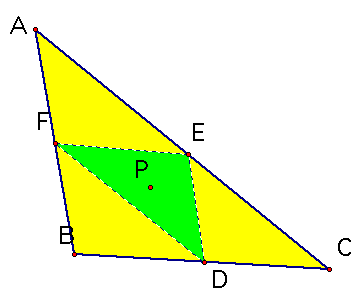
What makes this ratio equal to 4? We know that the medial triangle is 1/4 the area of the original triangle, so when our three segments form the medial triangle we have a ratio of 4 to 1. Where would our point P have to be inorder to form the medial triangle? The centroid of course!

Return to Home Page