

Write the parametric equations of a line segment through (7,5) with a slope of 3. Graph the line segment using your equations.
Using algebra, we can determine the y - intercept needed to write the cartesian equation of the line containing the point (7,5) with a slope of 3
Since the y- intercept is -16 and the slope is 3, the cartesian equation is y = 3x - 16.
To write this equation parametrically, we need another point on the line segment. If I let x = 8, then y = 8 using our cartesian equation. We can determine parametric equations as follows:
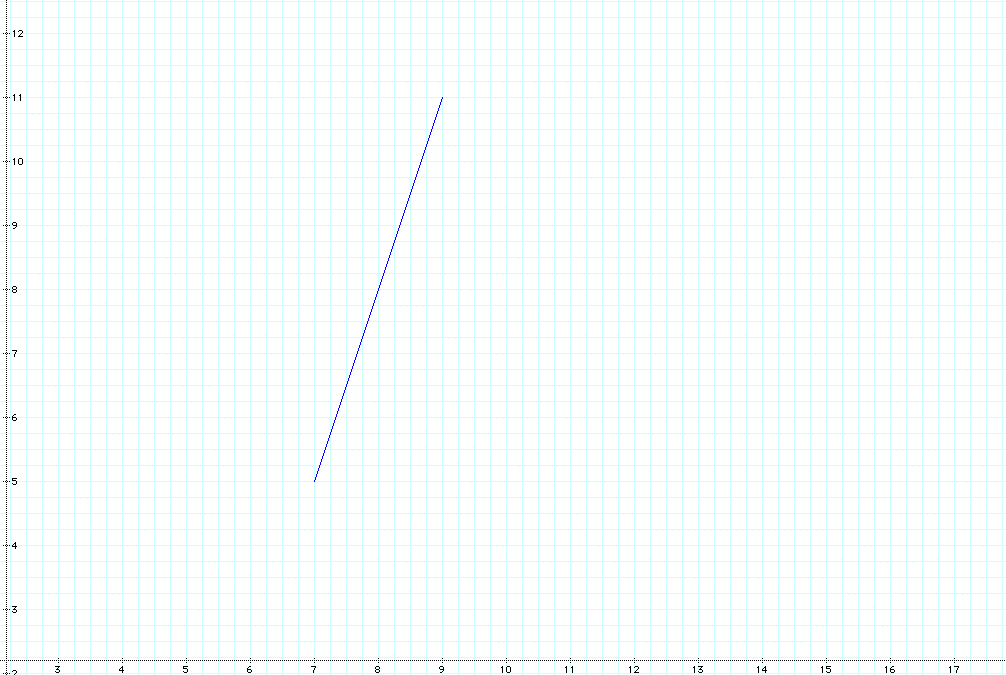
The graph yields a line segment for values of 0 < t < 2.
Suppose we chose the point (5, -1). How would that change the parametric equations? How would that change the graph?
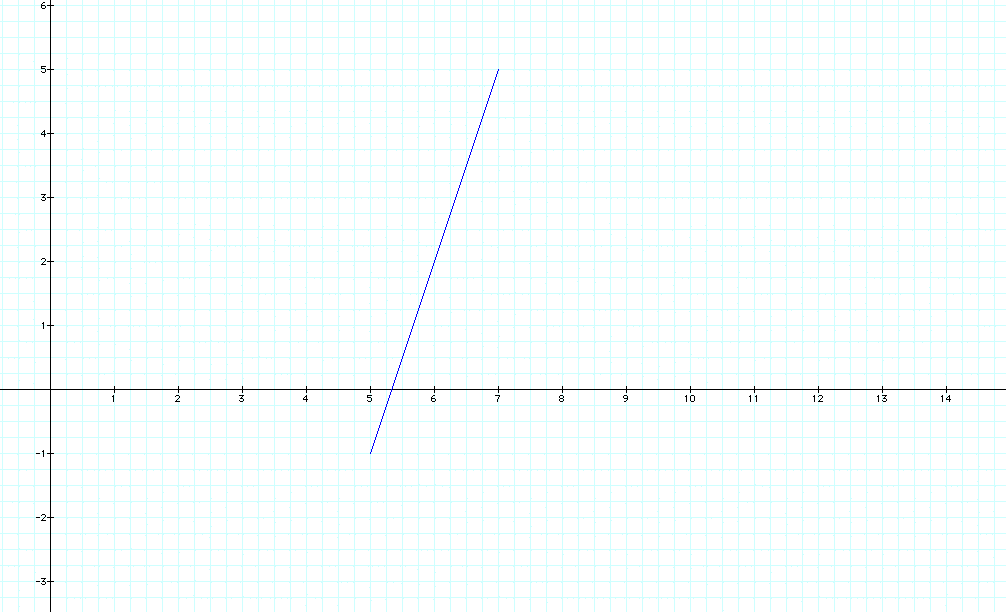
The segment produced has the point (7, 5) as the endpoint, but the segment still lies on the line y = 3x - 16.