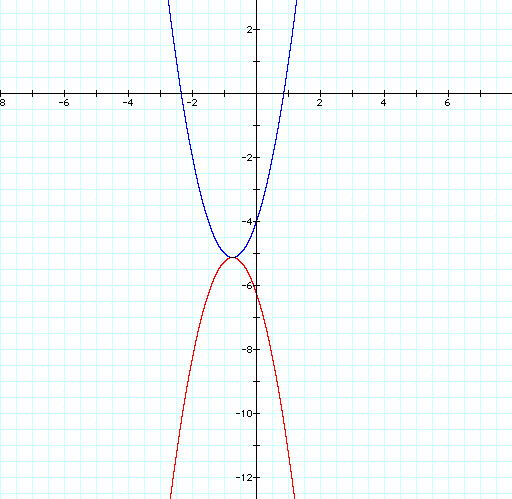
Graph
i. Overlay a new graph replacing each x by (x - 4).
ii. Change the equation to move the graph into the second quadrant.
iii. Change the equation to produce a graph
concave down that shares the same vertex.
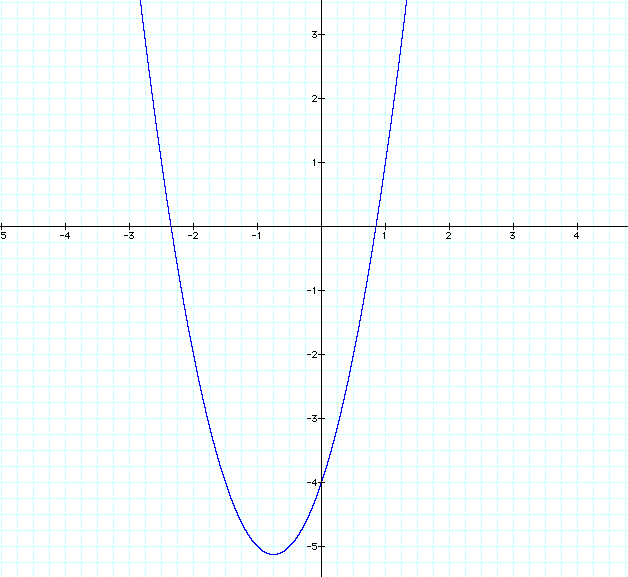
This graph represents a quadratic function with a vertex at (-.75, -5.125).
i. What happens to the graph when x is replaced with (x-4)?
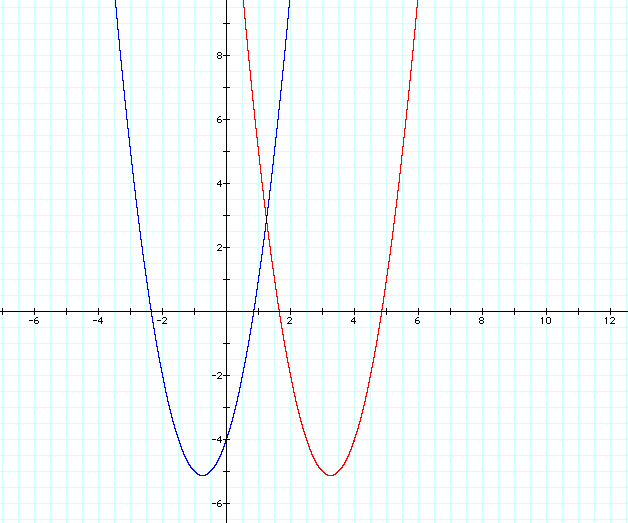
Notice that by replacing x with (x - 4), the quadratic curve (parabola) is moved, or it is translated 4 units to the right, creating a new quadratic function with a vertex at the point (3.25, -5.125). In general, replacing x with x - h will translate the graph h units to the left (when h < 0) or h units to the right (when h > 0).
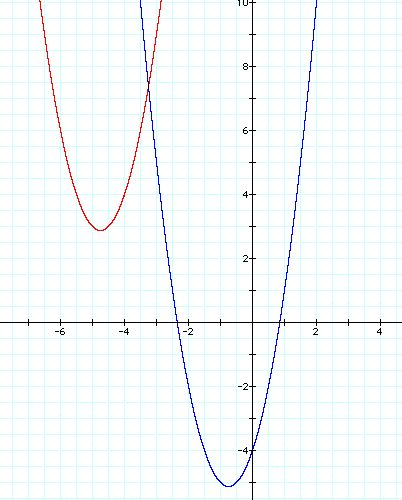
ii. To move the graph to the second quadrant (where the x-values are negative and the y-values are positive), we must consider the following: we need to translate the graph vertically so that the y-coordinate of the vertex is positive, or above the x-axis. Therefore, we need h < 0, and we need to change -4 to +4 for a positive vertical shift:
iii. For a quadratic function, a concave down graph would be a reflection of all points that define the graph across the x-axis. If both parabolas have the same vertex, the reflection of the original would have to be translated vertically by the distance between the two vertices.