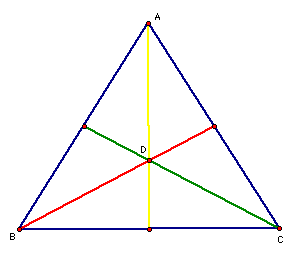
The centroid of a triangle is the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side. Point D is the centroid of triangle ABC.
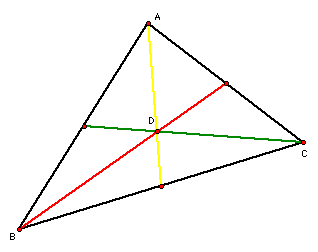
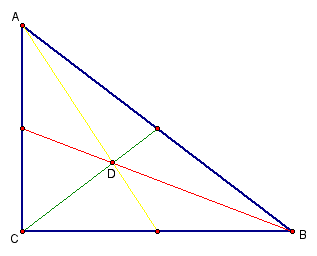
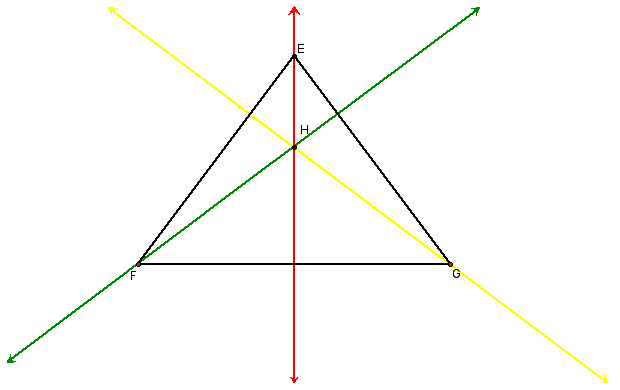
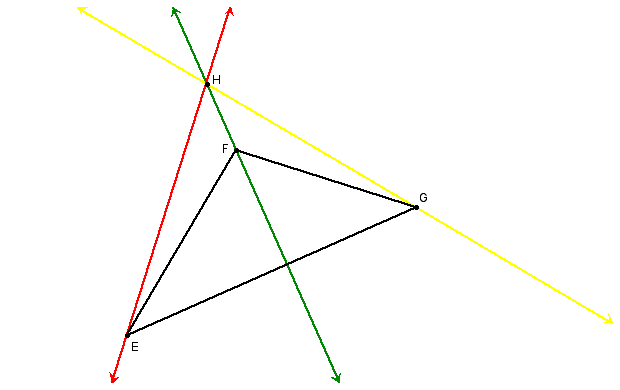
The orthocenter of a triangle is the common intersection of the three lines containing the altitudes. Below, point H is the orthocenter of triangle EFG.
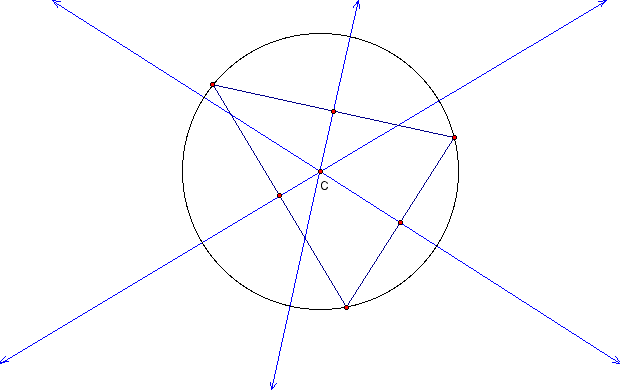
The circumcenter of a triangle is the point in the plane that is equidistant from the three vertices of the triangle. The circumcenter is on the perpendicular bisector of each side of the triangle. Point C is the circumcenter of the triangle below:
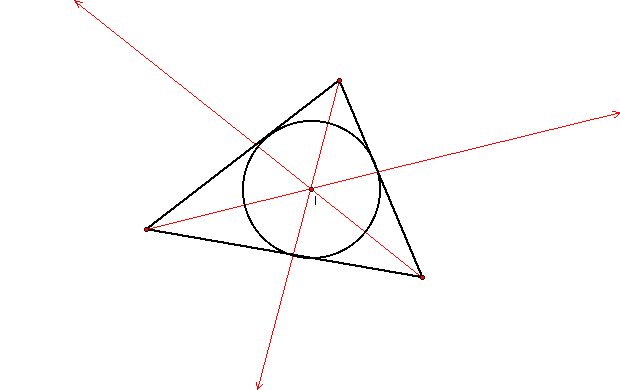
The incenter of a triangle is the point on the interior of the triangle that is equidistant from the three sides. The incenter lies on the angle bisector of each angle. Point I is the incenter of the triangle below:
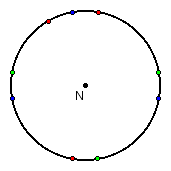
The Nine Point Circle for any triangle passes through the three midpoints of the sides (green points), the three feet of the altitudes (red points), and the three midpoints of the segments from the respective vertices to the orthocenter (blue points).
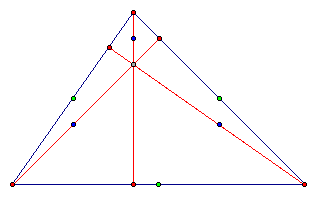
The following is the Nine Point Circle for the triangle above, with center N: