Assignment 12

Investigation 7

Using Data to Make Predictions

We have an experiment that was done with the following parameters.

Take a cup of hot water and measure its initial temperature (time = 0) and then record temperature readings each minute for 30 minutes. Make note of the room temperature.

Now we can make a spreadsheet with the data as follows.

Time Temperature
0 212
1 205
2 201
3 193
4 189
5 184
6 181
7 178
8 172
9 170
10 167
11 163
12 161
13 159
14 155
15 153
16 152
17 150
18 149
19 147
20 145
21 143
22 141
23 140
24 139
25 137
26 135
27 133
28 132
29 131
30 130

We can also use the data to create a function that will model the data. First we plot the data, and then plot a regression line. The equation of our regression line is .

Now we can use the function to predict the temperature after 45 minutes, 60 minutes, or 300 minutes, simply by plugging in 45, 60 or 300 into our equation. So the temperature will be about 99.21 at 45 minutes, about 78.63 at 60 minutes, and about 1.9 at 300 minutes.

We can also calculate a measure of the error between our model and the observed data by taking the square of the difference for each time, sum the squares, and divide by the number of data points. We can use this statistic to guide refinement of our function to model the data.

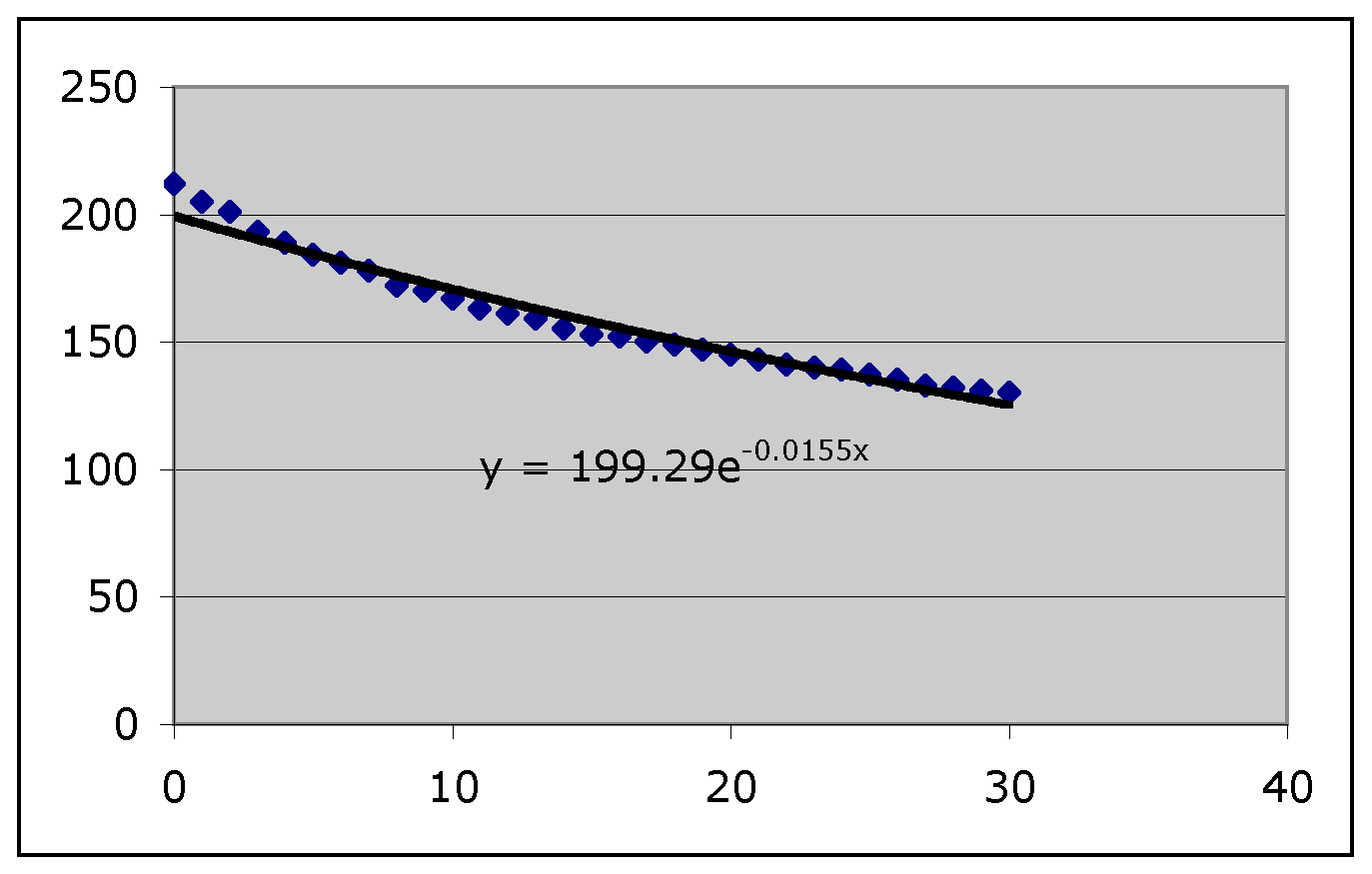
Time Temperature Predicted Value Difference Squared difference Sum of squares Error
0 212 199.29 -12.71 161.5441 555.738644157322 18.5246214719107
1 205 196.224821500553 -8.77517849944715 77.0037576971595
2 201 193.206786958321 -7.7932130416788 60.7341695129925
3 193 190.235171275989 -2.76482872401061 7.64427787311415
4 189 187.309260508596 -1.69073949140389 2.85860002779268
5 184 184.428351692006 0.428351692005748 0.183485172044187
6 181 181.591752674018 0.59175267401784 0.350171227207264
7 178 178.798781948074 0.798781948074151 0.638052600569135
8 172 176.048768489523 4.04876848952341 16.3925262817577
9 170 173.341051594405 3.34105159440458 11.1626257564734
10 167 170.674980720709 3.67498072070933 13.5054832975853
11 163 168.049915332086 5.04991533208636 25.5016448612409
12 161 165.465224743949 4.46522474394936 19.9382320139777
13 159 162.920287971952 3.92028797195206 15.368657783032
14 155 160.414493582794 5.41449358279374 29.3167407581146
15 153 157.947239547319 4.94723954731941 24.4751791385612
16 152 155.517933095879 3.51793309587944 12.3758532670839
17 150 153.125990575914 3.12599057591382 9.771817080702
18 149 150.770837311727 1.77083731172678 3.13586478460373
19 147 148.451907466418 1.45190746641819 2.10803529104089
20 145 146.168643905939 1.16864390593861 1.36572857888745
21 143 143.920498065235 0.920498065234966 0.847316688101316
22 141 141.706929816455 0.706929816455414 0.499749765393685
23 140 139.527407339181 -0.472592660819259 0.223343823060228
24 139 137.381406992652 -1.61859300734773 2.61984332343496
25 137 135.268413189964 -1.73158681003562 2.99839288068934
26 135 133.187918274192 -1.81208172580767 3.28364018100611
27 133 131.139422396425 -1.86057760357463 3.4617490189235
28 132 129.122433395676 -2.8775666043245 8.28038956232363
29 131 127.136466680634 -3.86353331936647 14.9268897098549
30 130 125.181045113244 -4.81895488675647 23.2223262005941

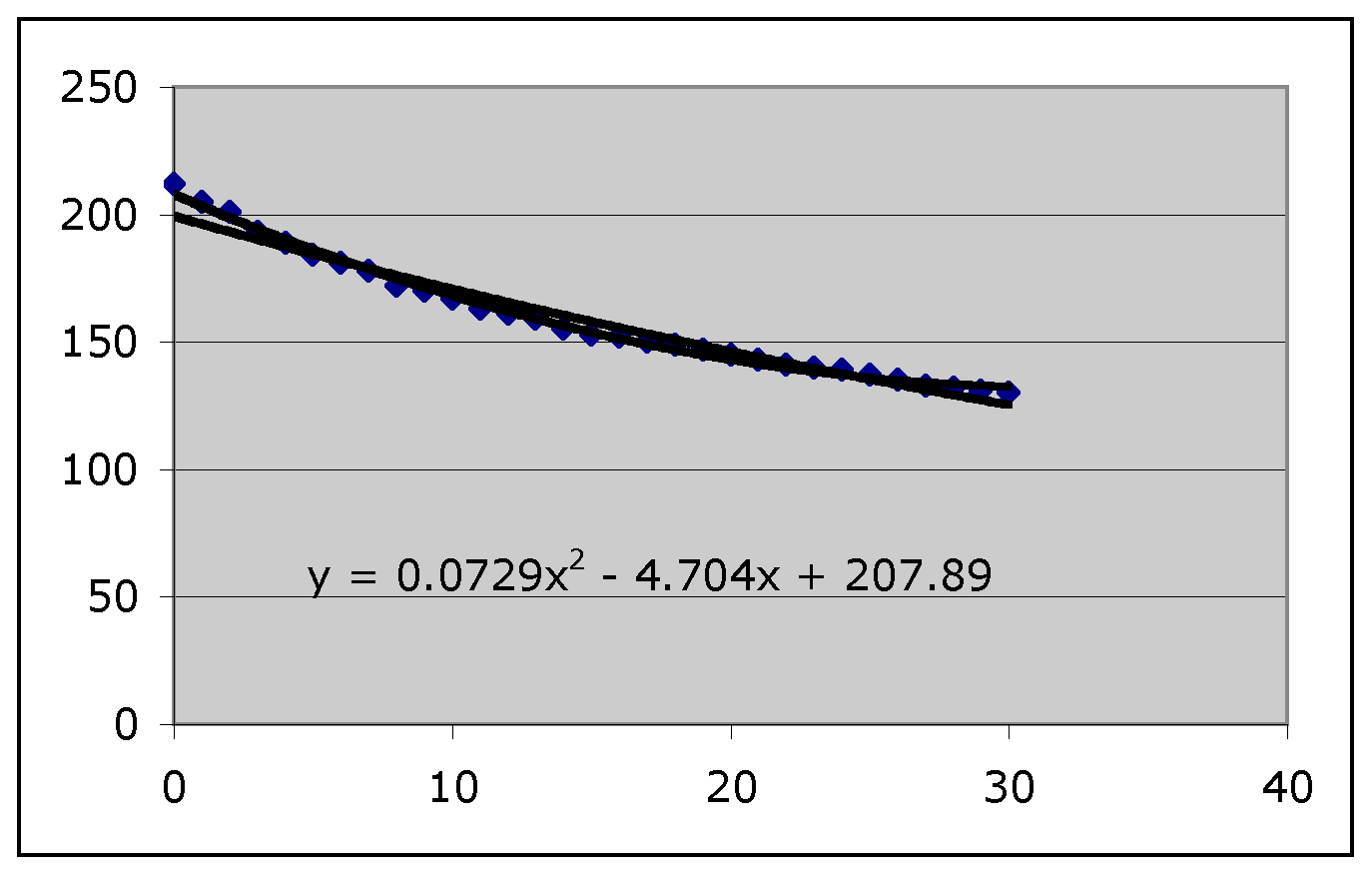
So our error is about 18.5 which is not very good. So lets try a different trend line and equation.

If we calculate the error with this new equation we get a much better result.

Time Temperature Predicted Value Difference Squared difference Sum of squares Error
0 212 207.89 -4.11000000000001 16.8921000000001 94.1365955899999 3.13788651966666
1 205 203.2589 -1.74110000000002 3.03142921000006
2 201 198.7736 -2.22640000000001 4.95685696000005
3 193 194.4341 1.4341 2.05664281
4 189 190.2404 1.24039999999999 1.53859215999998
5 184 186.1925 2.1925 4.80705624999998
6 181 182.2904 1.29039999999998 1.66513215999994
7 178 178.5341 0.534099999999995 0.285262809999995
8 172 174.9236 2.92359999999999 8.54743695999996
9 170 171.4589 1.45889999999997 2.12838920999992
10 167 168.14 1.13999999999999 1.29959999999997
11 163 164.9669 1.96689999999998 3.86869560999993
12 161 161.9396 0.939599999999984 0.882848159999971
13 159 159.0581 0.058099999999996 0.00337560999999954
14 155 156.3224 1.32239999999999 1.74874175999997
15 153 153.7325 0.732499999999987 0.536556249999982
16 152 151.2884 -0.711600000000004 0.506374560000006
17 150 148.9901 -1.00990000000002 1.01989801000003
18 149 146.8376 -2.16239999999999 4.67597375999996
19 147 144.8309 -2.16910000000001 4.70499481000006
20 145 142.97 -2.03 4.1209
21 143 141.2549 -1.74510000000001 3.04537401000003
22 141 139.6856 -1.31440000000001 1.72764736000002
23 140 138.2621 -1.7379 3.02029640999999
24 139 136.9844 -2.01560000000001 4.06264336000002
25 137 135.8525 -1.14750000000001 1.31675625000002
26 135 134.8664 -0.133600000000001 0.0178489600000003
27 133 134.0261 1.02609999999999 1.05288120999997
28 132 133.3316 1.33160000000001 1.77315856000002
29 131 132.7829 1.78289999999998 3.17873240999994
30 130 132.38 2.38 5.66439999999998

Our new error is only 3.14. So our new equation is a much better fit of our curve, and therefore, much more useful in predicting future data sets.

Return to Assignment 12