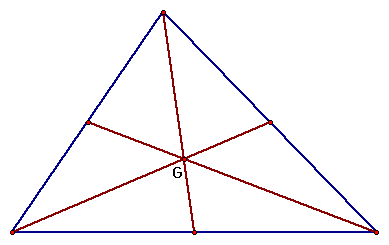
The CENTROID (G) of a triangle is the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side.

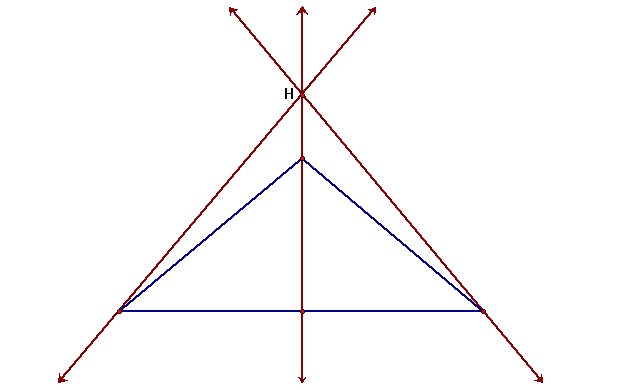
The ORTHOCENTER (H) of a triangle is the common intersection of the three lines containing the altitudes. An altitude is a perpendicular segment from a vertex to the line of the opposite side. (Note: the foot of the perpendicular may be on the extension of the side of the triangle.)
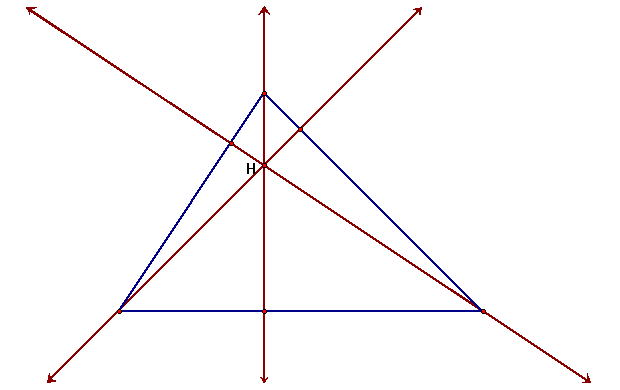
It should be clear that H does not have to be on the segments that are the altitudes. Rather, H lies on the lines extended along the altitudes. The triangle below demonstrates this.
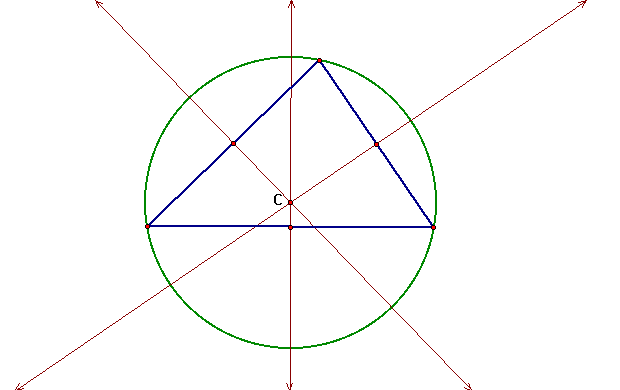
The CIRCUMCENTER (C) of a triangle is the point in the plane equidistant from the three vertices of the triangle. Since a point equidistant from two points lies on the perpendicular bisector of the segment determined by the two points, C is on the perpendicular bisector of each side of the triangle. Note: C may be outside of the triangle.
The INCENTER (I) of a triangle is the point on the interior of the triangle that is equidistant from the three sides. Since a point interior to an angle that is equidistant from the two sides of the angle lies on the angle bisector, then I must be on the angle bisector of each angle of the triangle.
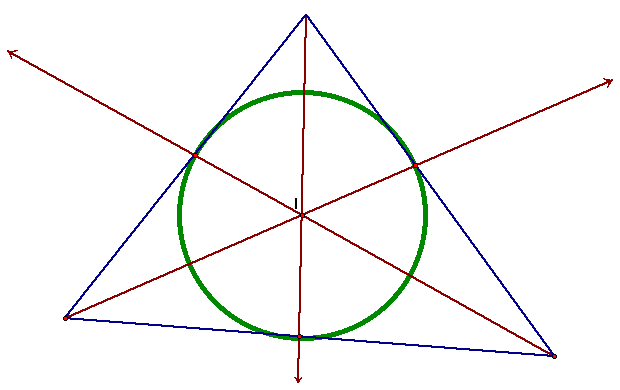
If we plot G, H, C, and I all on the same triangle we can explore the relationship between them for different triangles. We can see in an acute triangle, the four points appear to be collinear.

As we shift the triangle to the left or right, we can see the G and I remain fairly close to each other, while C and H get further apart.
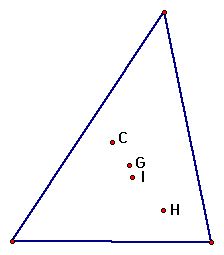
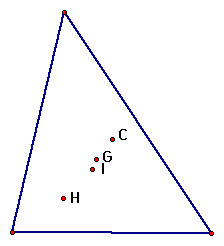
Click HERE to see the triangle shift randomly on the plane.
When we have a right triangle, the points lay in particular places. H is on the vertex where we have the right triangle, and C is the midpoint of the hypotenuse.

We can also see that when we have an obtuse triangle, H and C are outside of the triangle.
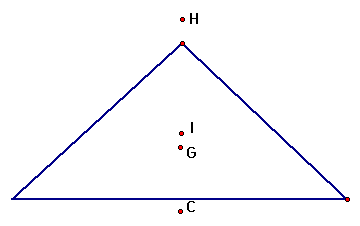
And when we have an equilateral triangle, the three points are the same.
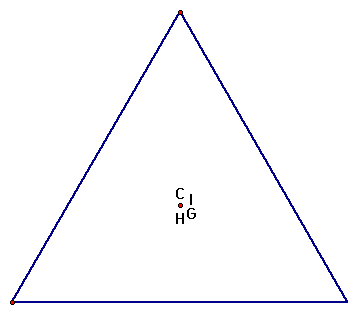
We can also see that no matter what type of triangle we have the H, G, and C are always collinear. Click HERE to see the line segment that H, C and G are always on.