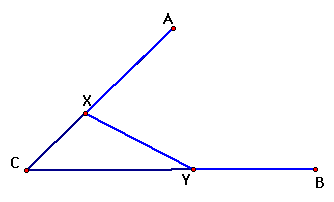
Given three points A, B, and C. Draw a line intersecting AC in the point X and BC in the point Y such that
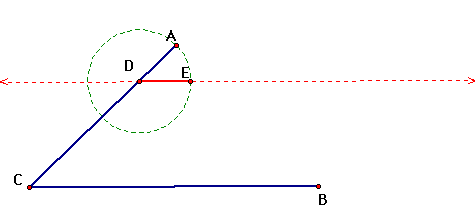
We start out by choosing a point D on AB. Then with the point D and the line segment BC we can create a new line. Then by using a circle, we can create a point E such that AD = DE
Now if we create a triangle by connecting A and B, we can then draw a line segment from E to a point F on the segment AB such that DE = EF
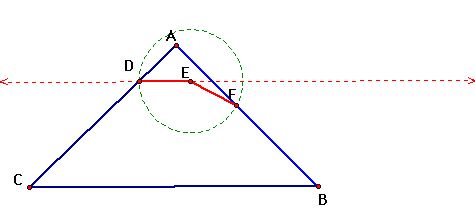
Now we can construct a rhombus with sides DE and EF.
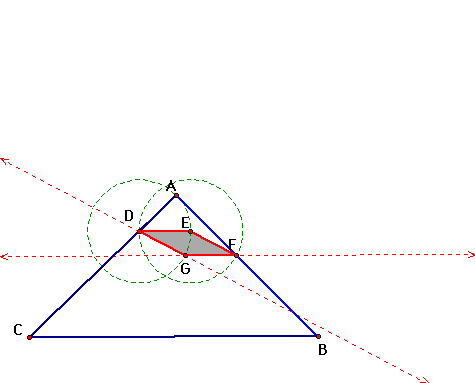
And we notice that the point G is on the circle with center D and radius AD, so we know AD=DG=EF.
Now if we hide everything except our original lines, and line segments DG and GF we can see our picture much more clearly.
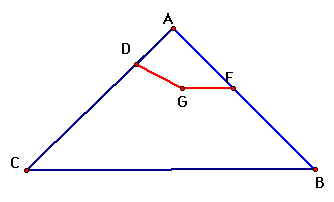
Now we want to draw a line through A and G and label the point where the line intersects CB as Y.
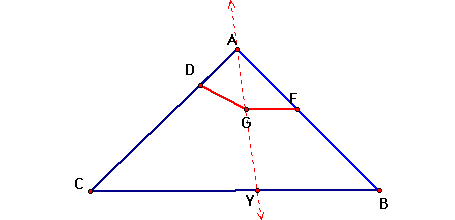
Now by creating a line segment parallel to DG, we can create a new point on AC where the segments intersect. Let's name the new point X.
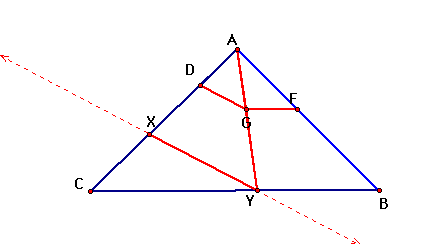
If we look at similar triangles we can see triangle AXY is similar to triangle ADG, and also triangle AYB is similar triangle AGF.
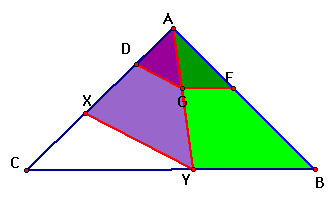
Now from our similar triangles, we can see that the following ratios hold true.
and
But we can see that two sets
of rations share the ratio 
, so we can set
any of the five equal to each other. For example, we can say the
following.
But if we remember from our construction we know AD=DG=GF, so we can conclude AX=XY=BY.
