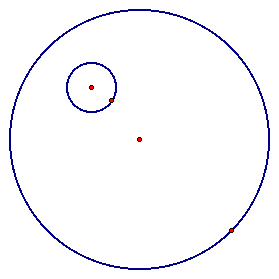
If we are given two circles and a point on one of those circles, we can construct a third circle that is tangent to both original circles with one point of tangency being the designated point.

Click HERE for the script to create the third circle, tangent to the original two.
But we can also create a fourth circle that is tangent to the original two between the two circles. Click HERE to see the script.
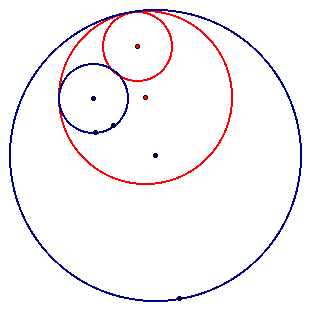
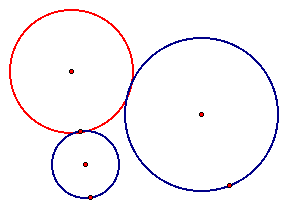
We can also use these scripts to see that when the smaller circle is outside the larger circle for both tangent circles.
 or
or 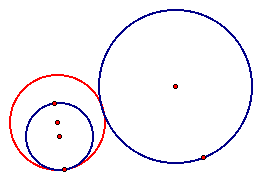
We can also use the script tools to see what the tangent circles look like when the two original circles intersect.
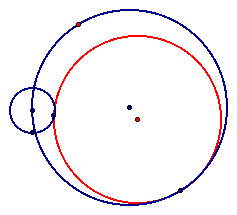 or
or 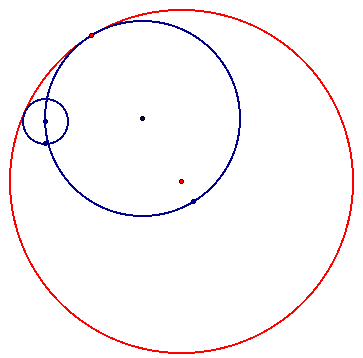
Now we will explore the locus of the centers of all such circles tangent to the two given circles. We will begin with the first circles we created when the smaller circle was inside the larger circle.
We can see that the locus of the center of the first circles are elipses. Now lets explore the locus of the center of the tangent circle when the smaller circle is outside the larger circle.
We can see that the locus of the centers of the circles are hyperbolas when the smaller circle is outside the larger circle. Now lets look at when our original circles intersect.
We see when the two original circles intersect the locus of the center of the tangent circle acts differently for the inner tangent circle then it does with the outer tangent circle. The locus of the inner tangent circle looks like the locus when the circles were inside each other as an eclipse, and the locus of the outer tangent circle looks like when the smaller circle was outside the larger circle as a hyperbola. This is very interesting since when the circles were inside each other or disjoint, both the inner and outer tangent circles had similar locus.