We begin by constructing a triangle ABC.

Now we can construct an orthocenter, H for triangle ABC.
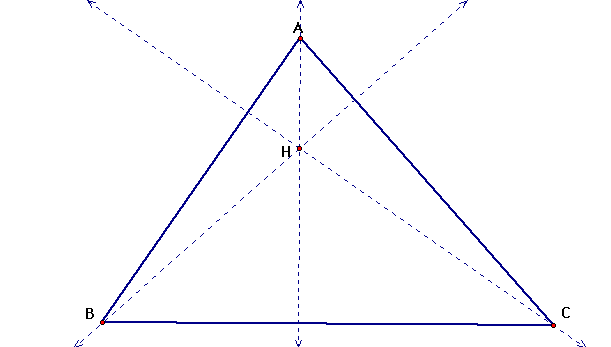
Now we will create triangle HBC, and find its orthocenter.
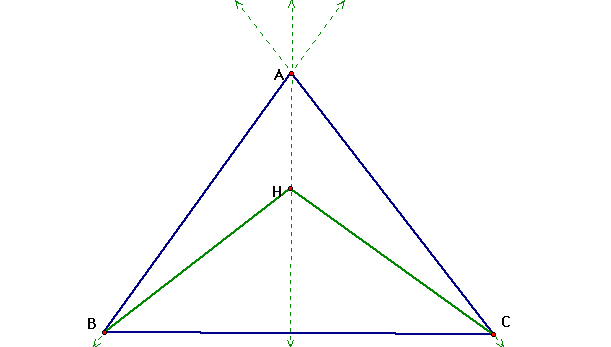
It is easy to see that the orthocenter of HBC is the point A. Now lets see where the orthocenter of triangle HAB.
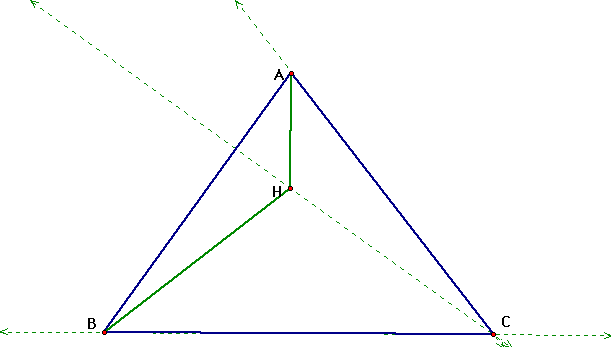
It is easy to see that the orthocenter of HAB is the point C. Now lets see where the orthocenter of triangle HAC.
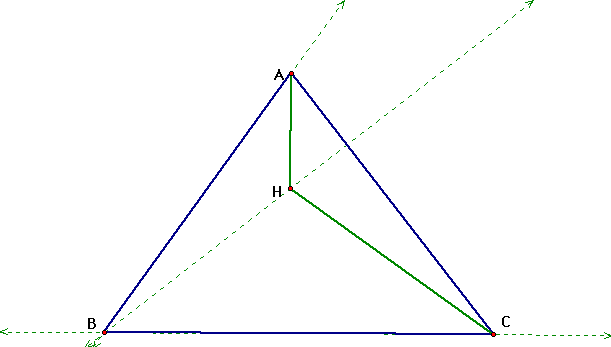
Just as we expected, the orthocenter of triangle HAC is the point B. Now if we put all of our triangles on the same drawing, and construct the circumcircles we get the drawing below.
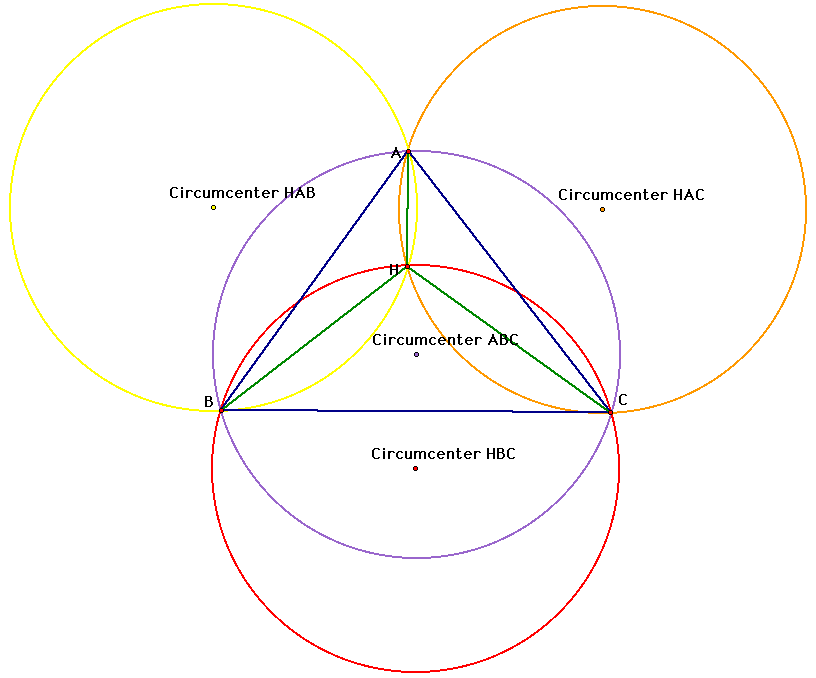
Lets see how our picture would change if one of the vertices of our original triangle, say A was moved to where the orthocenter is.
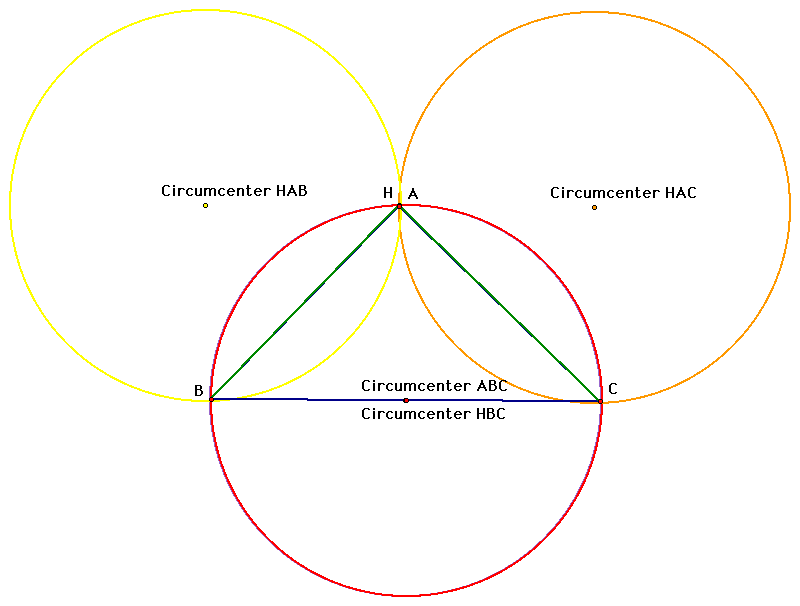
We can see that our circumcircles for HBC and ABC are now the same because triangles HBC and ABC are now the same. Now lets look at the nine point circles for these triangles. Below is the nine point circle for our original triangle ABC.
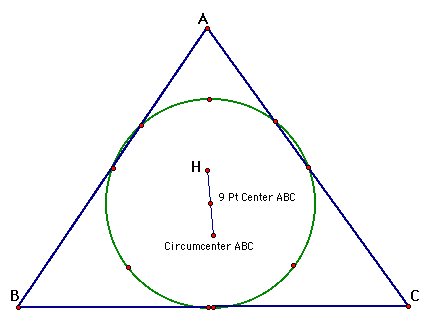
Now we can create a triangle HBC and examine the nine point circle for it.
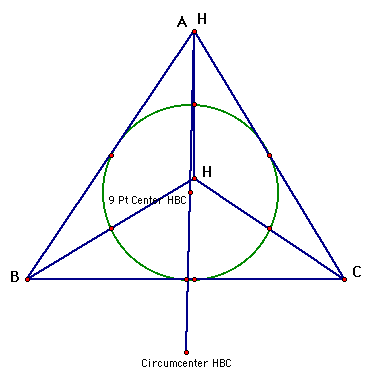
Now lets look at triangle HAC, and HAB and see what their nine point circles look like.
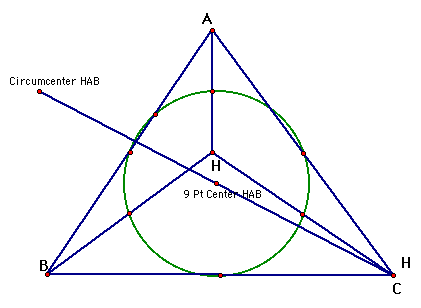
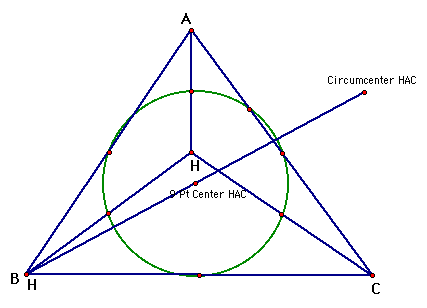
If we put all three nine point circles on the same picture, we can see that they are all the same.
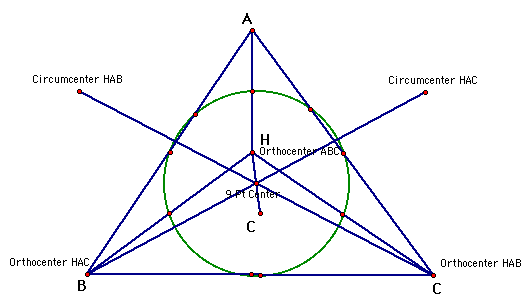
Now let's look at the original triangle and it's incircle, three excircles, and its nine point circle.
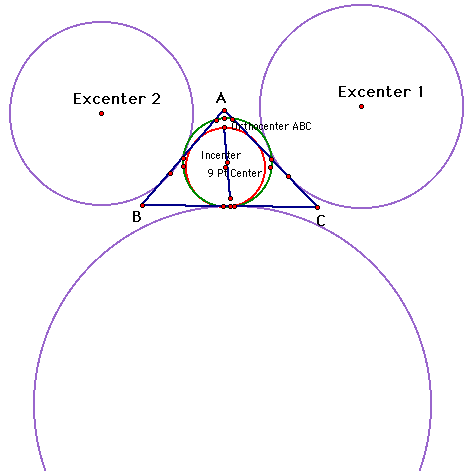
We can see that depending on the triangle there is at least one point on the triangle that is tangent to the incircle, the nine point circle, and one of the excircles.
Now we can take our original triangle ABC, and construct altitudes, and its circumcircle. We will label the points where the altitudes meet the circumcircle D, E and F.
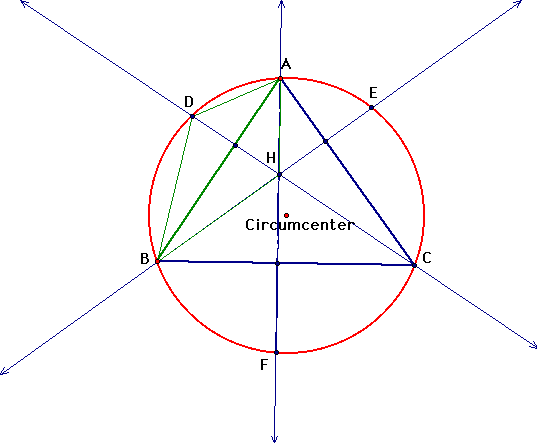
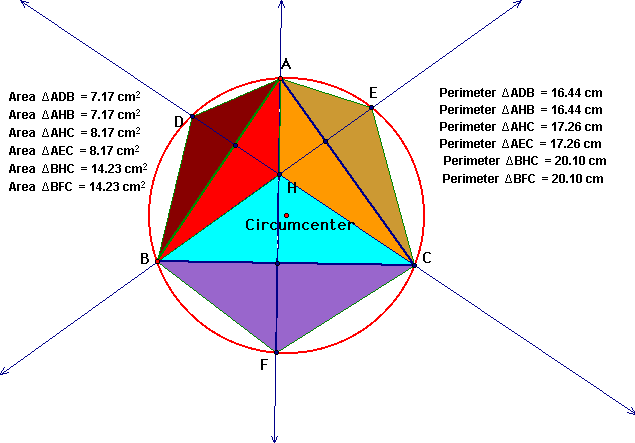
We can then compare the triangles formed with the new points and the triangles formed with the orthocenter. Triangle ABD is a reflection of triangle ABH. And the same is true for Triangles AEC and AHC and CBF and CBH.
We also see an interesting correlation between the ratios of the altitudes of the original triangle, and the extended altitudes that meet the circumcircle.
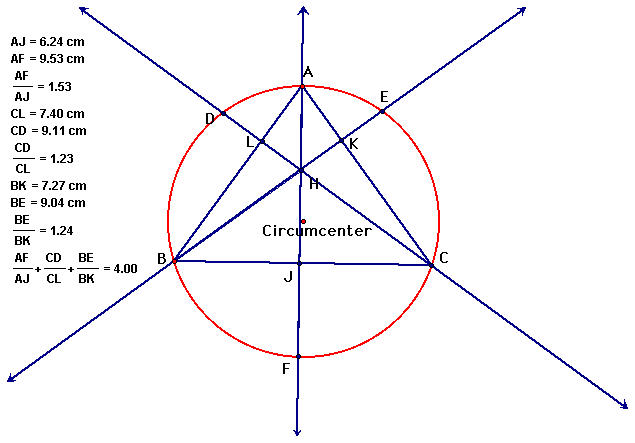
Even if we change the original triangle ABC to any acute triangle the sum of the ratios is always 4.
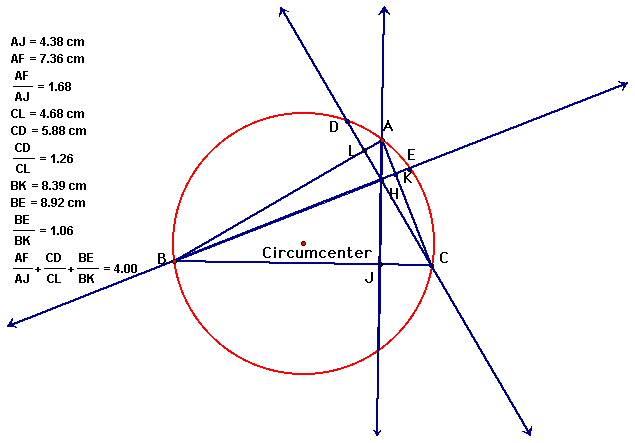
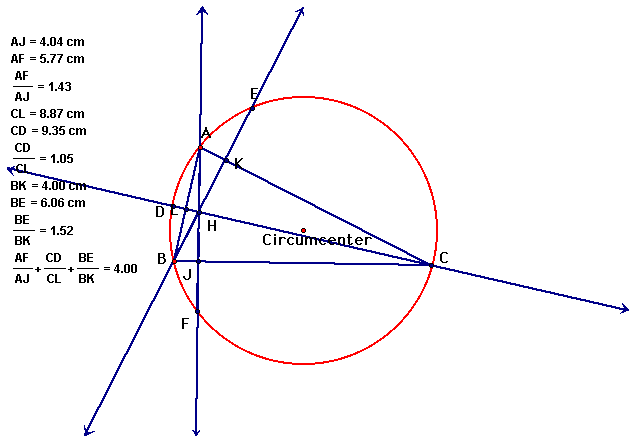
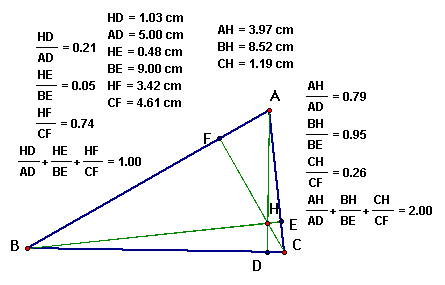
We can also see a correlation between any triangle and the ratios of the segments formed with the orthocenter and the altitudes of the triangle.
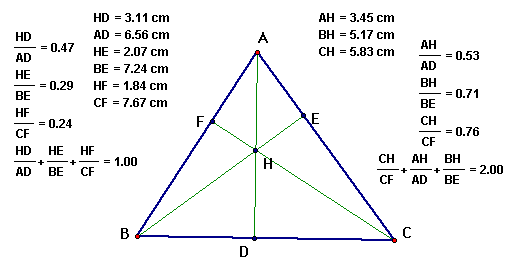
We can see that even when we change our original triangle ABC to any acute triangle the ratios remain the same.
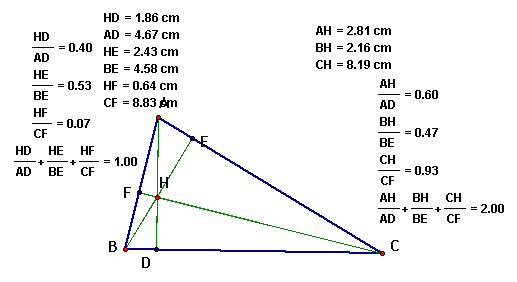
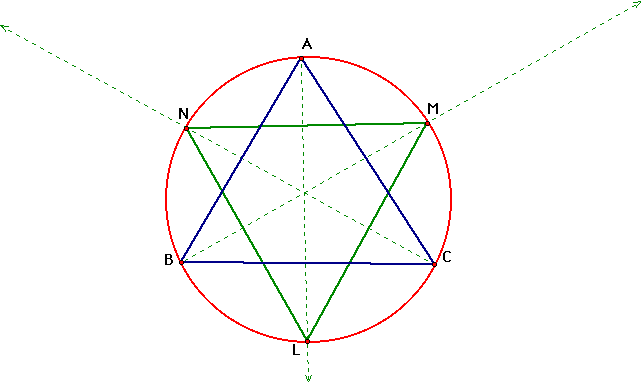
Now lets explore the angle bisectors and the circumcircle. If we go back to our original triangle ABC and construct angle bisectors for angle A, B and C, and extend them to meet the circumcircle at points L, M, and N respectively, we create the following construction.
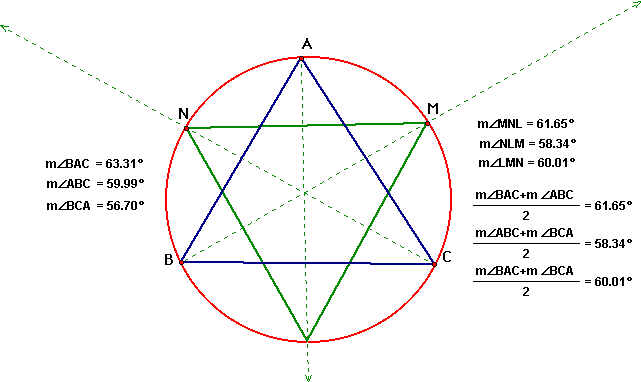
Since we know that angles that cut off the same chords of a circle are congruent we know that each of the angles L, M, and N are equal to half of the two angles of triangle ABC on each side of it. For example angle L is the same as one half of angle B plus C.
Now we will construct the orthocenter of triangle ABC and then construct the circumcircle of the new triangle ABH. The if we reflect our original triangle ABC across AB we create a new triangle ABC'.
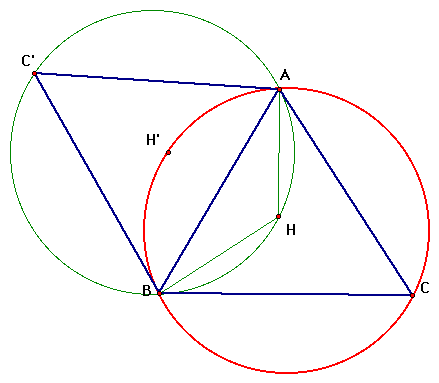
Since C' is also on the circumcircle we can see that we have also created a rhombus C'ACB, and therefore we can prove that the angles L, M, and N are half of the sum of the two surrounding angles.