Final Assignment
Semians and Similar
Triangles
If we take any triangle ABC,
and select a point P inside the triangle and draw lines AP, BP,
and CP extended to their intersections with the opposite sides
in points D, E, and F respectively, we get a construction like
the one below.
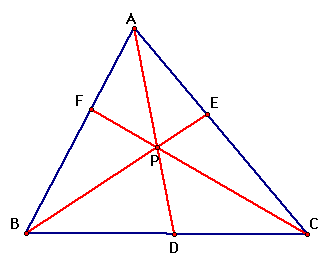
Now we want to explore the connection
between the semians FB, DC, and EA; and AF, BD, and, EC.
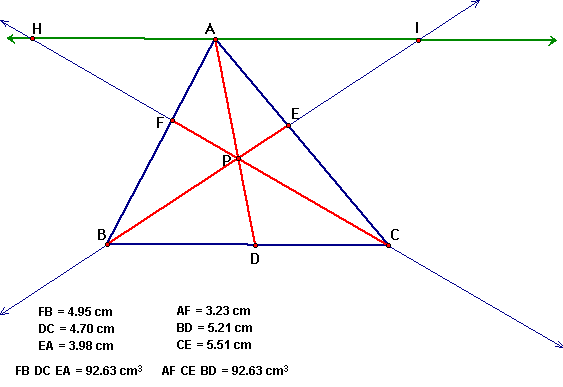
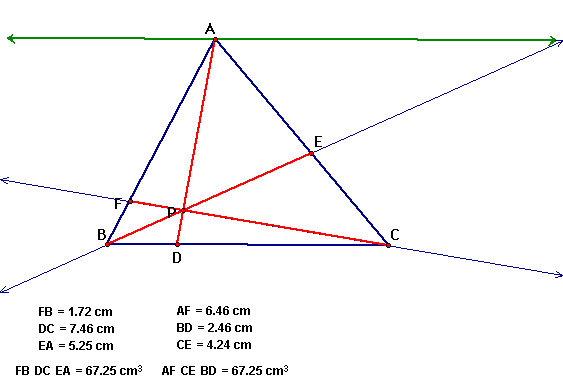
We can see that even when we
move P, the result is the same FB*DC*EA=AF*CE*BD.
If we want to prove the above
conjecture, we begin by constructing a line parallel to BC through
the point A, and then extend the lines AC and AB so they intersect
our new line through A. Label the points of intersections H and
I.
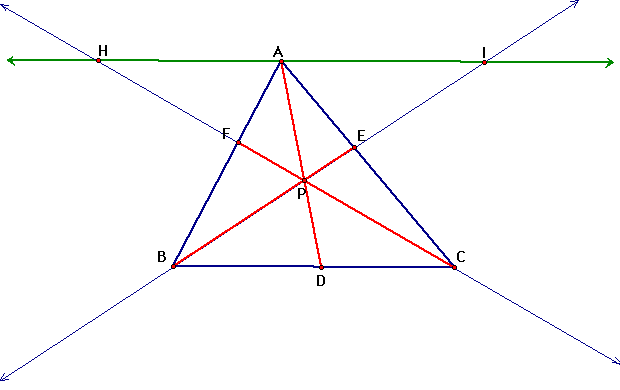
Now since we have parallel lines
and intersecting lines we can conclude that the following triangles
are similar.
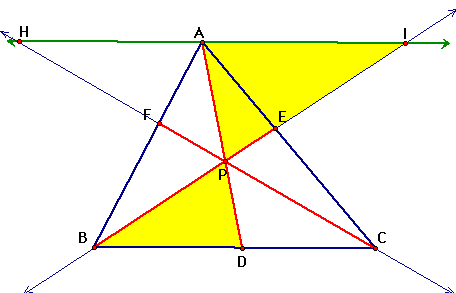
Triangle BPD is similar
to triangle IPA
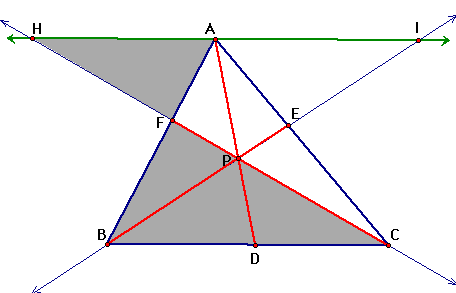
 Triangle HAP is similar
to triangle CDP
Triangle HAP is similar
to triangle CDP
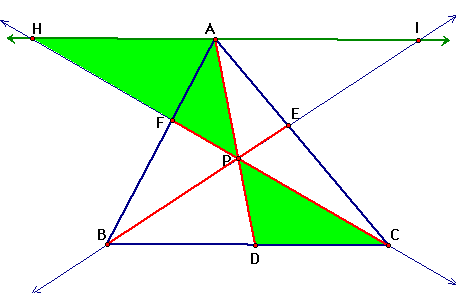 Triangle AEI is similar
to triangle CEB
Triangle AEI is similar
to triangle CEB
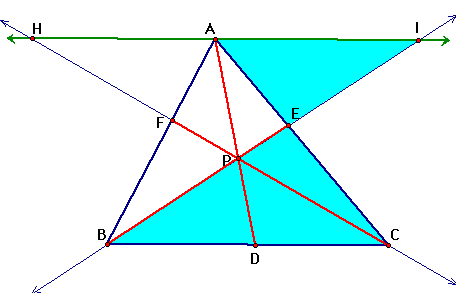 And triangle HFA is similar
to triangle FCB
And triangle HFA is similar
to triangle FCB
 Now we can conclude that
the following ratios are true
Now we can conclude that
the following ratios are true
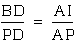 since triangles BPD and IPA are similar.
since triangles BPD and IPA are similar. 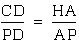 since
triangles HAP and CDP are similar.
since
triangles HAP and CDP are similar.
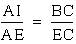 since triangles AEI and CEB are similar.
since triangles AEI and CEB are similar. 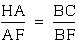 since
triangles HFA and FCB are similar.
So when we do a little
manipulation of our ratios we see the following
since
triangles HFA and FCB are similar.
So when we do a little
manipulation of our ratios we see the following
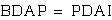 so
so 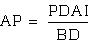 and
and
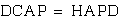 so when we plug in AP from above, we get
so when we plug in AP from above, we get 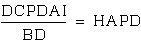 also
also
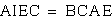 so
so 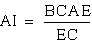 , so when we plug this into our
equation above we get
, so when we plug this into our
equation above we get 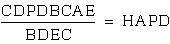 and also
and also 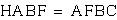 so
so 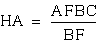 and we can put this into our equation,
and get
and we can put this into our equation,
and get 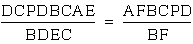 .
Now when we rearrange
our equation we get
.
Now when we rearrange
our equation we get 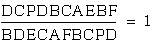 and our PD's and BC's
cancel, so we have
and our PD's and BC's
cancel, so we have 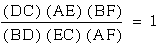
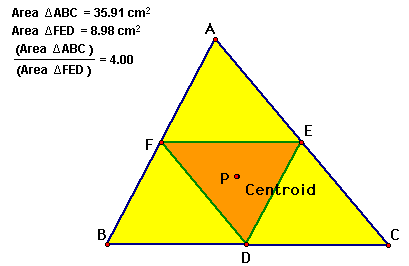
We can also see a relationship
between the triangle ABC and the new triangle formed by D, E,
and F.
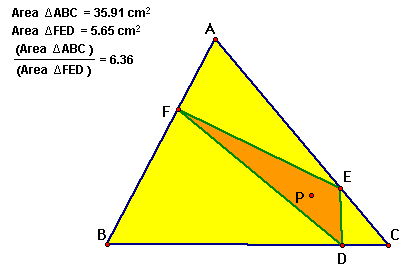
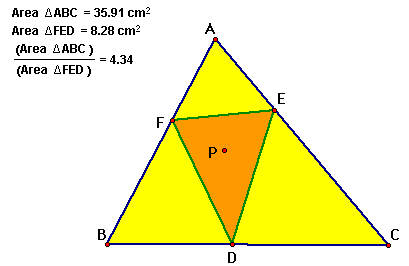 No matter where we move
P to the ration of the area of triangle ABC to the area of triangle
FED is greater than or equal to 4.
No matter where we move
P to the ration of the area of triangle ABC to the area of triangle
FED is greater than or equal to 4.
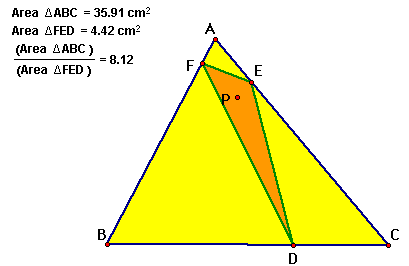 And when the ratio is
equal to four, we notice that P is the centroid of triangle ABC.
And when the ratio is
equal to four, we notice that P is the centroid of triangle ABC.
Return
to Stacey's Page













