

Graphs of the equation ![]() yield parabolic curves where a does not equal
zero. By changing each of the values a,b, or c while holding the
other two constant we may observe what particular effect changes
in each one of these values has on the graph of the parabola.
So lets begin by varying the constant term c. This yields the
graphs pictured below. (The color of the graph corresponds to
the color key on the equations.)
yield parabolic curves where a does not equal
zero. By changing each of the values a,b, or c while holding the
other two constant we may observe what particular effect changes
in each one of these values has on the graph of the parabola.
So lets begin by varying the constant term c. This yields the
graphs pictured below. (The color of the graph corresponds to
the color key on the equations.)
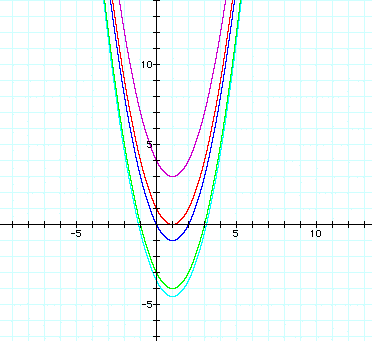
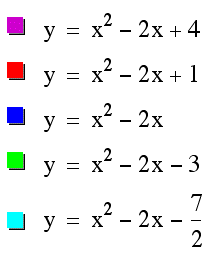
Looking at the five graphs and the five equations it is readily apparent that changes in the value of the constant term c move the entire graph of the parabola vertically only. As c decreases in value the graph is shifted down. It is shifted down (at the vertex point) a number of spaces which corresponds to the difference in the c values. We may notice two other things of importance. The constant term always describes the y intercept of the graph. This is algebraically obvious as well because substitution of 0 for x will yield the constant term in each case, but it is nice to note that what we obviously see also readily falls out algebraically. The other thing to note is that the graph doesnt undergo any horizontal shift, nor does the parabola "close in" or "spread out". Pictorially these are changes we might imagine happening. How might we effect these changes? We have 2 more coefficients to work with.
Lets continue by changing the varying the value of b and holding a and c constant. We might take a look at the graphs of the equations below.
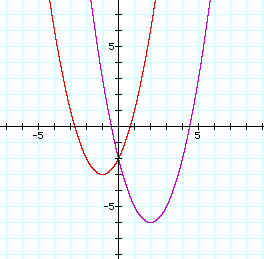
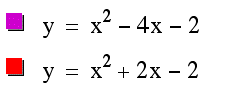
In this case changing the value of b while holding a and c constant yields a horizontal shift in the graph (notice the x value of the vertex has shifted). Interestingly as the coefficient b gets larger the graph appears to shift to the left, which might be different than we would guess or suspect. A vertical shift has also taken place here, and so to effect a horizontal shift only, we must use what we learned in the first section of this discussion and bring the graph of the second equation down. We do this by decreasing the value of c. It is our belief that we must decrease c by 3 from looking at the graph. Lets graph our new equations and see what happens.
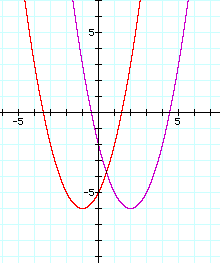
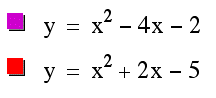
Algebraically we could confirm this need to alter the top equation by subtracting 3. We complete the square on each of the equations, subtract the amount that was necessary to complete the square from the constant term and notice a difference in the 2 equations of 3. The algebra again confirms the geometry.
Of course we could have raised the other graph by adding to c, but the main point to understand here is that we can effect a directly horizontal change in the graph by techniques we have learned. Now let us look at changes in a while holding b and c constant.
We now look at our last coefficient. Lets look at a couple of equations and their graphs.
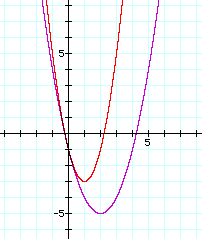
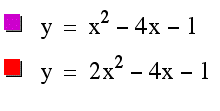
Again increasing a has shifted the graph up and to the left. Or has it? It certainly has shifted the vertex point up and to the left, however upon careful inspection we see that the entire graph of the lower equation exists within the graph of the upper equation. The second graph is "narrower" than the first. We speculate that if we decrease the value of a rather than increasing it, the graph will shift down and to the right and be "spread" more. Lets see if this holds true by adding another equation to our graph.
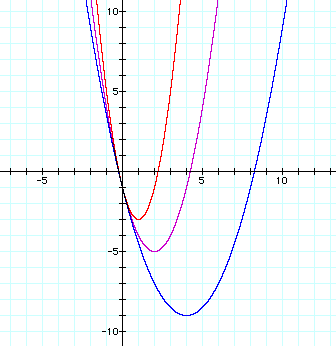
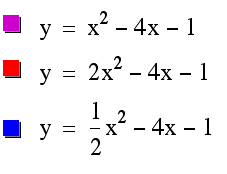
Finally, lets investigate negative values of a. We will change the top equation directly above by making a=-1. So the equation and graph are:
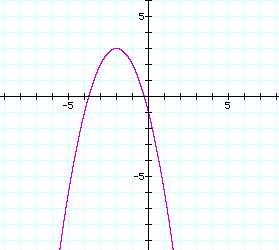
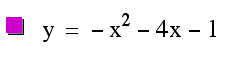
So a negative coefficient a turns the parabola upside down on the graph. In addition to this, in relation to the graph of the equation just like this one with the exception of a positive a, the graphs vertex is on the opposite side of the y axis.
As is usually the case with mathematics, an exploration of ideas opens up more problems than it answers. To just name one investigation suggested by this data, in the graphs where a was changing but positive, there appears to be a linear relationship between the vertex points. Does such a relationship exist? What line describes it in this case? How about the general case? Another day.......