

Lets begin this exercise by constructing any triangle abc, constructing the orthocenter H of abc and then the orthocenters of hbc,hab, and hac.
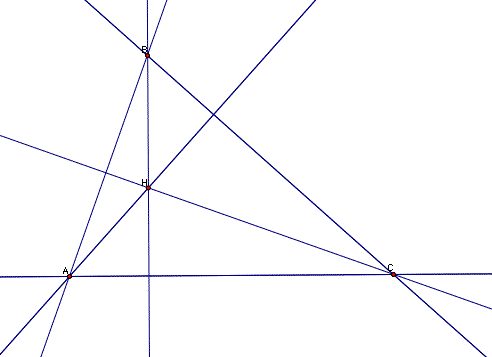
Given this picture, we can see by careful inspection rather than construction that the orthocenter of triangle HAB must be C. Likewise the orthocenter of HBC must be A, and the orthocenter of HAC must be B.Now let us proceed to construct the circumcircles of these triangles.

It would appear that all the circumscribed
circles are congruent. indeed this seems to be provable by the
fact that they all describe congruent arc lengths at their intersection
points, for example the light and dark green circles, both of
them describing equal ac lenghts which pass through points a and
b.