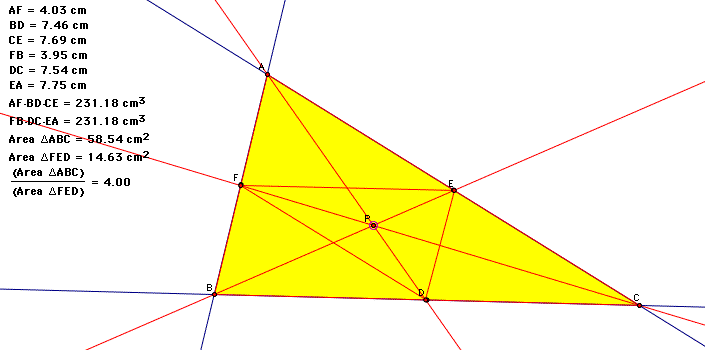
Lets choose a triangle of no particular type and a random point within the triangle and draw lines from each vertex point through the chosen point to an intersection with the opposite side.
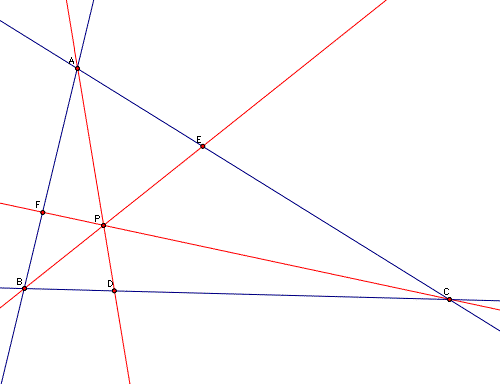
Using the measure tool in GSP we arrive at the following measurements:
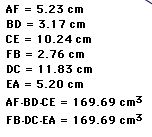
So we see that the two products are equal. We may make the conjecture that this will always be the case. For a working sketch in gsp to check the numerical validity of this conjecture click here.
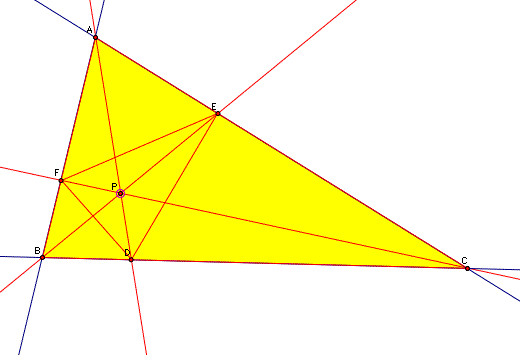
The calculation of the area of the triangles ABC and DEF are given here:
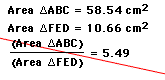
For a working gsp sketch which calculates the ratio of these areas for any point p in the interior of ABC click here.
This ratio will always be equal to or greater than 4. We would conjecture that the ratio would be equal to 4 when triangle DEF connects the midpoints of the sides of triangle ABC. A welll known theorem from geometry states that a segment connecting the midpoint of the sides is parallel to the thhird side and half as long.Lets check this out.