
Assignment 1
by Jeff Hall
8. Graph the equation
 where |x| is the absolute
value of x. Variations?
where |x| is the absolute
value of x. Variations?
The initial equation creates this graph:
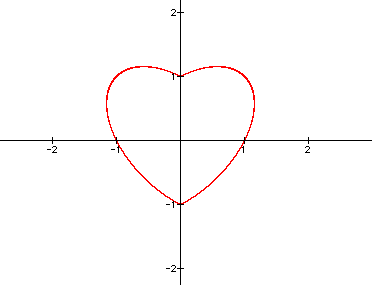 The equation creates
a heart-shaped figure that crosses
the x- and y- axes
at +1 and -1.
The equation creates
a heart-shaped figure that crosses
the x- and y- axes
at +1 and -1.
If you change the sign
in front of the first y, you get this equation and graph:

 The heart is the same
size and shape, but it is now inverted.
The heart is the same
size and shape, but it is now inverted.
Now let's change
the absolute value part so that the y is always positive.
Starting with the original
equation, I made the first y in the equation
be the absolute value
of y, and removed the absolute value sign
from the second x.
Here is the new equation and graph:

 The heart rotates clockwise 90 degrees.
The heart rotates clockwise 90 degrees.
What would happen if I changed
the sign in front of the absolute value of y?
At this point, I predict that changing
the sign will invert the heart again.

 As expected, the heart is inverted.
As expected, the heart is inverted.
Let's try something different. What
happens when you multiply
the middle portion of the equation
by the rational number n?
Here is the equation:
 where the value of n cycles from -5
through 5
Here is the graph of the heart with
the n value cycling from -5 through 5.
Note that when n equals zero, the heart
shape becomes a perfect circle.
Also note that the x- and y- intercepts
never change. Only the length and width
of the heart changes.
where the value of n cycles from -5
through 5
Here is the graph of the heart with
the n value cycling from -5 through 5.
Note that when n equals zero, the heart
shape becomes a perfect circle.
Also note that the x- and y- intercepts
never change. Only the length and width
of the heart changes.
What if you wanted to change the x-
and y- intercepts?
Consider what happened when n equaled
zero. Since the n would cancel out
the xy portion, the equation would
essentially become this:
 Using our knowledge of circles, we
know that changing the 1 would change the radius of the circle.
Would the same be true of our original
heart equation? Let's try it:
Using our knowledge of circles, we
know that changing the 1 would change the radius of the circle.
Would the same be true of our original
heart equation? Let's try it:
 where n cycles between 0 and 10.
Be still my beating heart!
where n cycles between 0 and 10.
Be still my beating heart!
Finally,
let's investigate what happens when both x and y are absolute
values.
Let's start with the original equation
and make the change:

 Now let's see it in motion with this
equation:
Now let's see it in motion with this
equation:
 where n cycles between
-10 and 2.
It is interesting to
note that this equation can be a diamond, square, or circle depending
on the n.
where n cycles between
-10 and 2.
It is interesting to
note that this equation can be a diamond, square, or circle depending
on the n.
Return






