Assignment 2

Problem #9 Write Up

by Jeff Hall
The graph of the first equation looks like this:

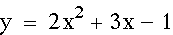
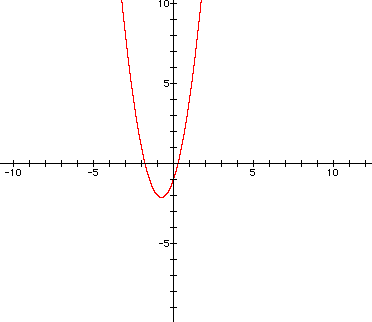This is a standard parabola.

Now let's add the second equation:

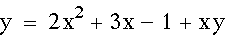
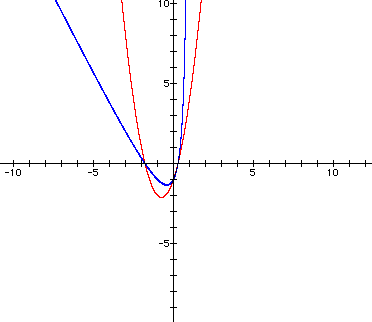The graph now looks like two parabolas crossing over one another. The red parabola is a standard parabola,

but the blue parabola is tilted at an unusual angle.
Are we getting the whole picture?

Since the blue parabola looks unusual, let's zoom out to see if anything else is going on.

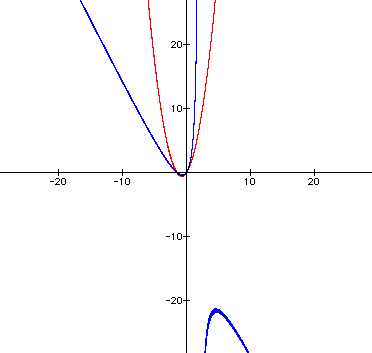As it turns out, we were not getting the whole picture before. When you zoom out,

you realize that the blue parabola we saw earlier was just part of the equation.

What would happen if I changed the coefficient in front of the xy variable? I predict that

the two blue parabolas will extend to meet each other.
In this next equation, I placed a 2 in front of the xy variable. Here are the equation and graph:

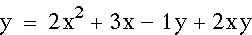
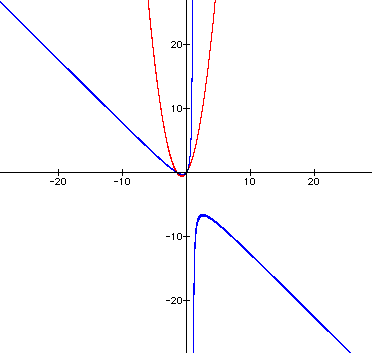The two parabolas are moving closer, but they are starting to get wider, too.

I predict that the parabolas will continue to grow wider and closer as the variable in front

of the xy (let's call it "n") increases.
Let's see what happens when I change the n from 2 to 10.

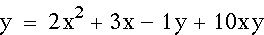
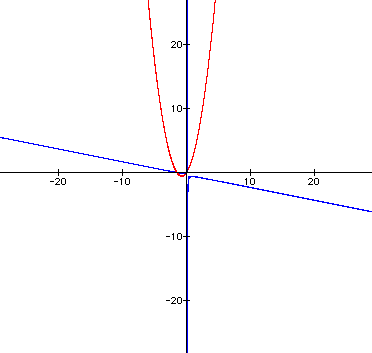As expected, the blue parabolas continued to get wider and closer to each other.

However, I am starting to suspect that the two parabolas will not actually connect with each other,

at least not with a positive n.
Let's try one more positive n just to be sure. Let n=100.

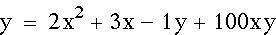
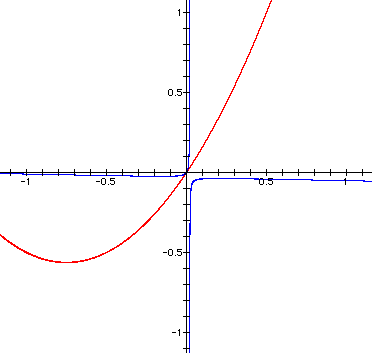Notice that I had to zoom in...a lot...in order to see what's happening here.

Our suspicions have been confirmed. The two parabolas will not connect when n is positive.
Let's try some negative numbers now. Let xy be negative.

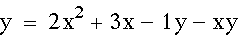
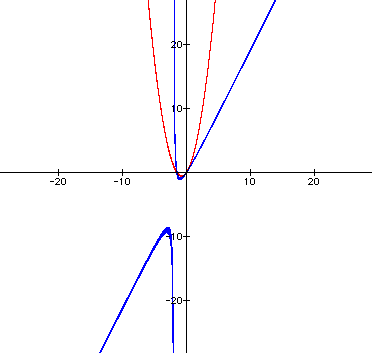The negative xy caused the parabolas to flip quadrants around a vertical axis.

Will the graphs of negative n-values continue to be a mirror-image of the positive n-value graphs?

Let's try n as -2.

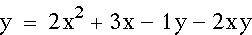
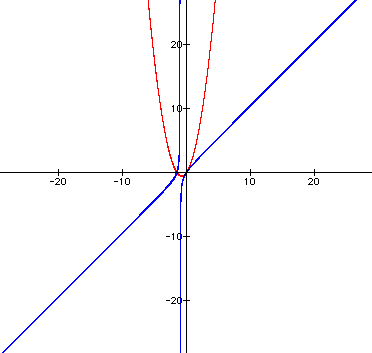Interesting. The two parabolas have shifted so that they form an hourglass shape.

This means that the two parabolas connected somewhere between n=-1 and n=-2.
What will the graph look like as n continues to get even more negative? Let's try n=-10.

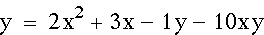
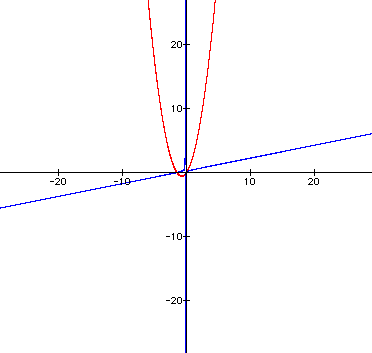The graph is again starting to look like a mirror-image of the positive n equations.
Let's try one last n just to be sure. Let n=-100.

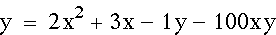
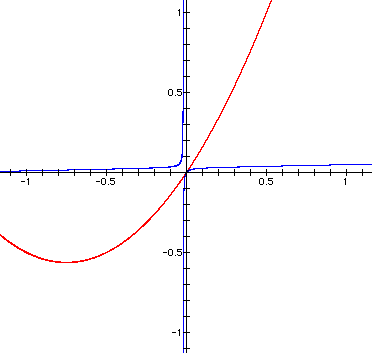Again, a close zoom was required to see the the two parabolas better.

As you can see, the two parabolas are not going to connect again as n approaches negative infinity.

We have explored the equation as n cycled from 100 to -100.

Let's see most of it together in one movie.

I placed the variable n, which cycles between -10 and +10, in front of the xy to get this equation and graph:

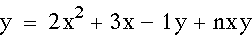Notice what happens when n=0. The blue and red parabolas are equal.

Notice also the point between n=-1 and n=-2 where the two parabolas finally connect before diverging again.

 

Return