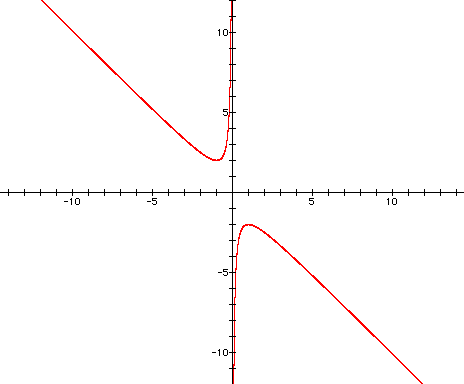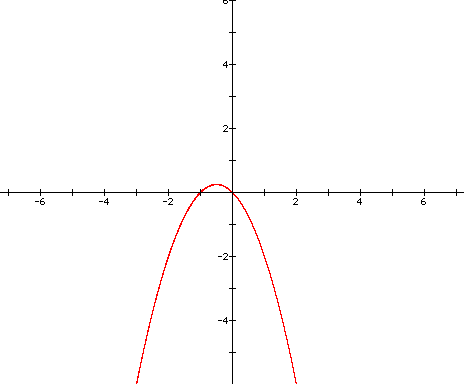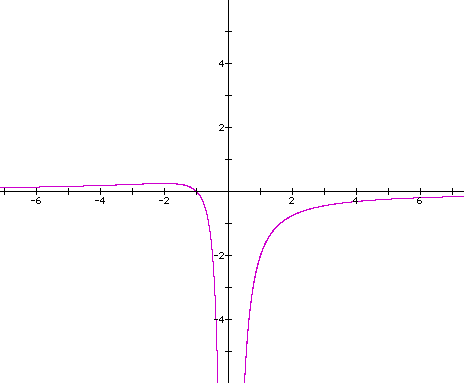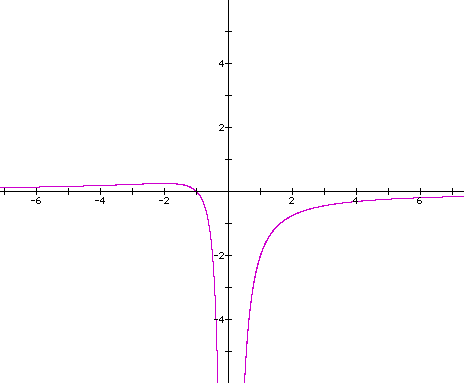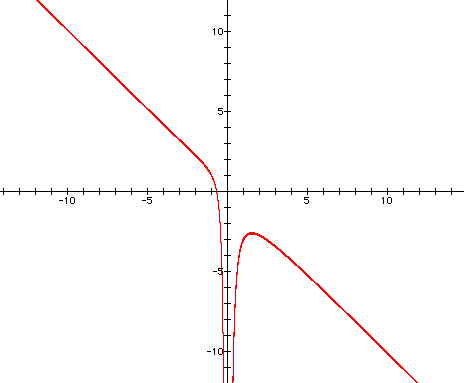Assignment 3

Quadratic and Cubic Equations

by Jeff Hall

Investigation #1

Let's investigate parabolas and the roots of equations. First, let's draw parabolas using the following equation:

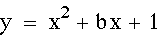for b = -3, -2, -1, 0, 1, 2, 3

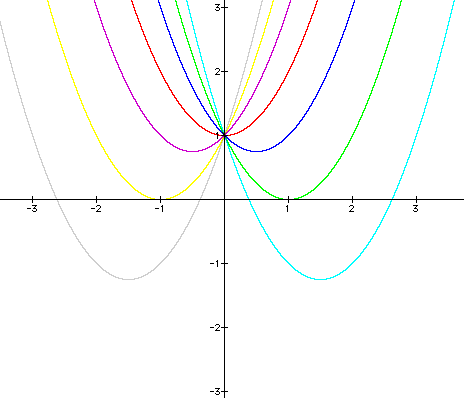As you can see, all of the parabolas cross the y-axis at (0,1). The roots of each equation occur when

each parabola crosses the

Now let's add another parabola:

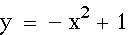
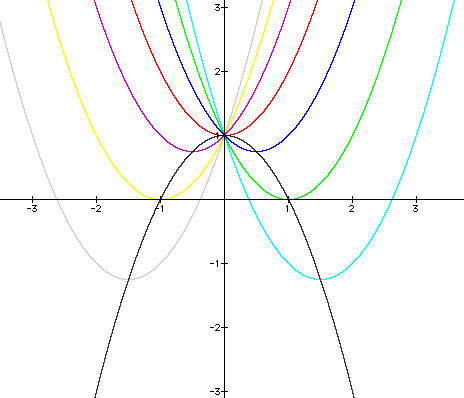The new parabola is colored black. It crosses the other parabolas at their loci.

Investigation #2

Here is an equation that we want graphed in the xb plane:

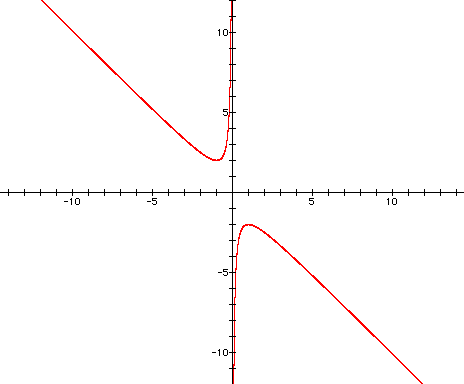
Now let's add a line where b=3

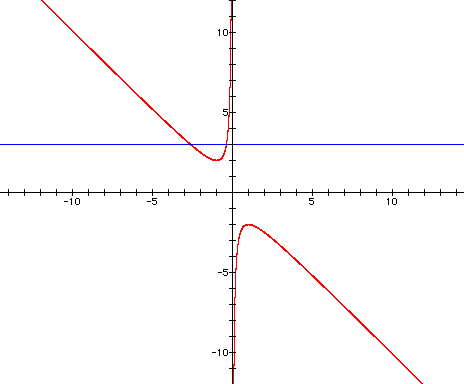The b=3 line crosses the original hyperbola at two points. These two points are the roots of the equation when b=3.
Let's zoom in and see how many roots we have when b=2:

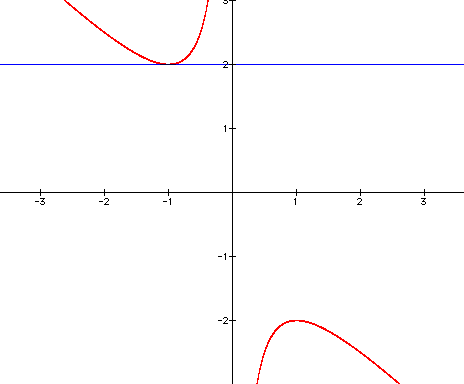As you can see, when b=2 there is only one root of the original equation.

It should now be clear that when -2<b<2, there are no roots at all.

Let's investigate what happens when the c variable changes. Let c=-1:

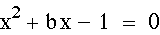
As you can see, when c=-1, the equation has exactly two roots at every variable b.
Now let's watch what happens as c cycles between -10 and 10:

As the c variable fluctuates, notice the amount of roots the equation has for each value b.
Investigation #3

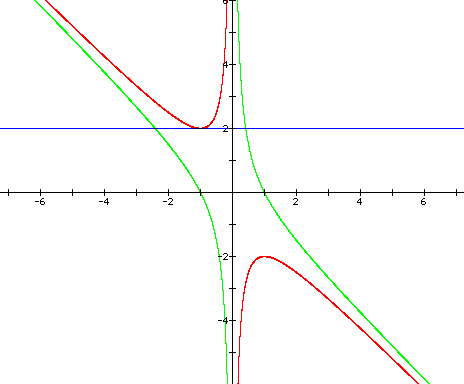
Now let's add another equation to this graph:

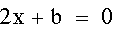
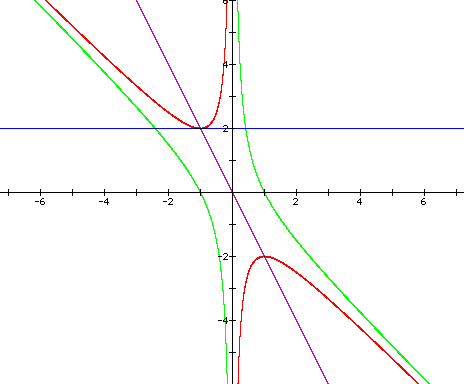What is the relationship of this equation to the quadratic formula?

This equation is the derivative of the first equation (drawn in red).

The local minimum and maximum are identified where these two equations cross.
Investigation #4

Since we just investigated graphs in the xb plane, let's try graphs in the xc plane.

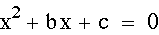
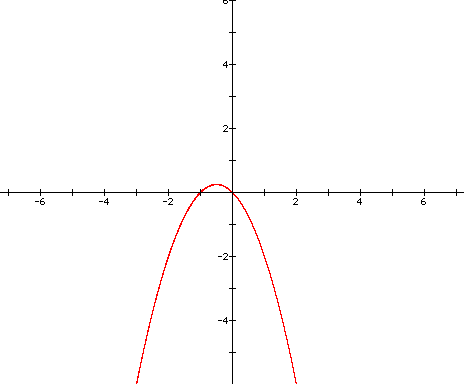
Let's add some equations to this graph. Let c=-2 to show the roots of the previous equation:

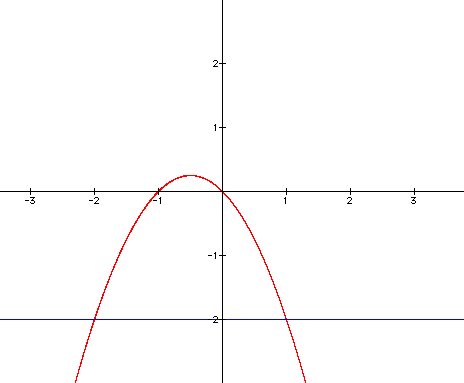
Now let's add the derivative of the first equation. It should intersect the parabola at its maximum point.

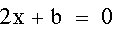
As expected, the derivative (drawn in purple) crosses the parabola at the maximum point.
Finally, let's watch what happens as c cycles between -10 and 10:

 

Notice that the maximum point becomes a minimum point as c becomes negative.
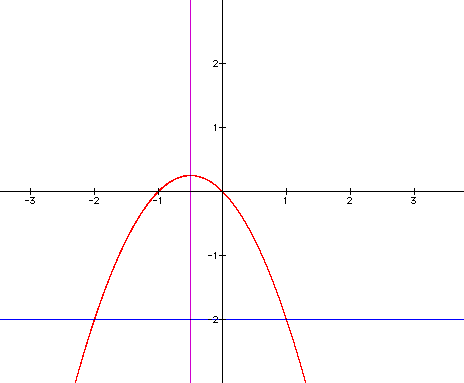
Now let's look at graphs in the xa plane, starting with the original equation again:

 

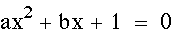
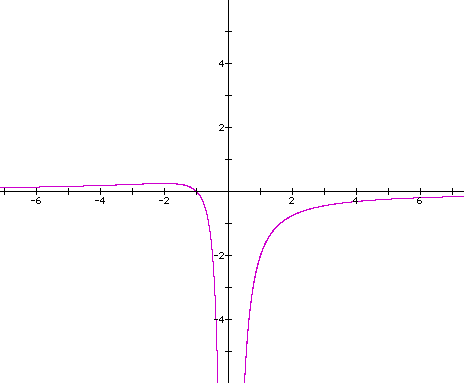
Now let's add a line where a=-1

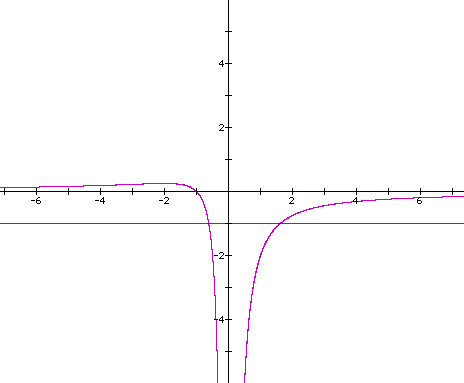As you can see, once again we get two roots when a=-1. However, notice how many roots are possible as

the a variable approaches zero. The number becomes infinite.
Now let's find the derivative of the equation:

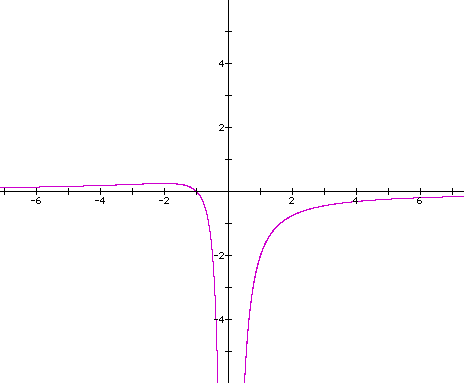
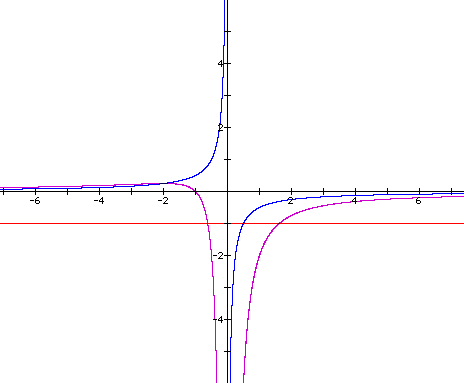Again, we see that the derivative (drawn in blue) crosses the original point at the local max and min points.
Finally, let's zoom in and watch as the variable a fluctuates between -10 and 10.

This time, I will also let the derivative equation fluctuate along with the original equation:

Investigation #6

Let's look at a new equation and graph it in the xb plane:

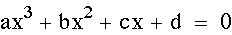
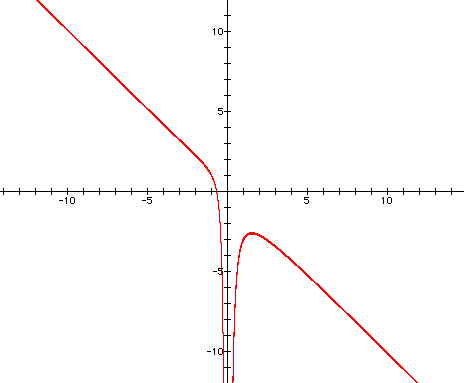An unusual looking graph...
Can you predict the maximum number of roots that this equation has?

Let's see how many roots there are at b=-5:

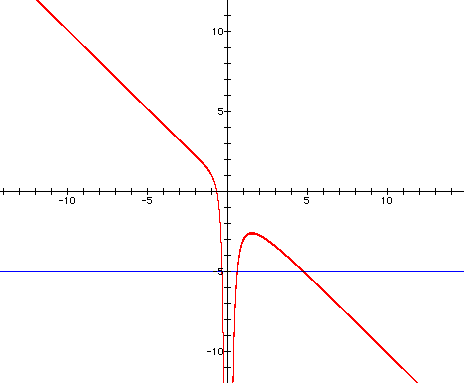As you can see, this equation yields a maximum of 3 roots. Why, you ask?

Well, I'll tell you! It's because this equation is a 3rd order quadractic equation.

Look at how the first x variable is cubed. This tells us that the maximum number of roots will be 3.
Now let's look at the derivative of the equation:

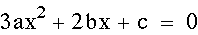
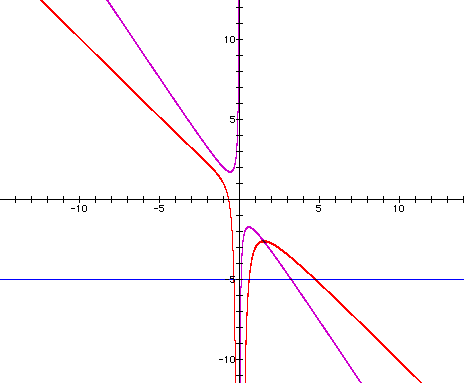This time, the derivative (drawn in purple) shows the local maximum for the parabola on the right,

but the curve on the left has no local min point, so the derivative does not cross it.
Finally, grab some popcorn and let's watch a movie of the equations as b cycles between -10 and 10:

 

Notice how the equations flip around the b-axis. Also notice how the derivative comes closer

to crossing the left curve as the absolute value of n gets larger.

That's what I call edge-of-your-seat excitement!

 

 

Return