Assignment 4

Quadratic and Cubic Equations

by Jeff Hall

Problem

Prove that the lines of the three altitudes of a triangle are concurrent

First, let's draw a picture of a triangle. I included the three altitude lines.

 

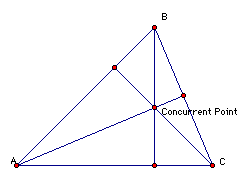The point where the three altitude lines cross is called the Orthocenter.

It is also a Concurrent Point because all three lines cross at this single point.

This illustrates that the three altitude lines are concurrent for this triangle alone.

Now let's prove it for all triangles.
Before we start our proof, we need to devise a strategy.

We know that perpindicular bisectors are concurrent at the centroid,

so if we could show that the orthocenter of one triangle is equal to the

centroid of a bigger triangle, we would prove that the orthocenter is

a point of concurrency for all triangles.

First, using parallel lines, create a larger triangle around the original.

 

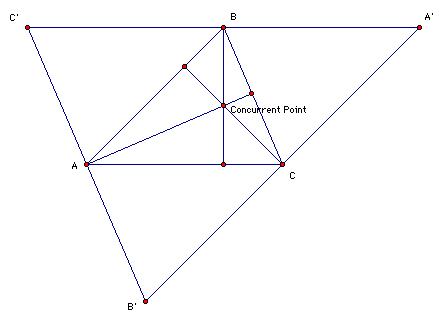I labeled the new vertices as A', B', and C'.

Notice that A, B, and C are now the midpoints of their respective segments.

The centroid, or the point of concurrency for perpindicular bisectors, is found

by connecting each vertex to their respective midpoint.

Here is the graph with the centroid drawn in:

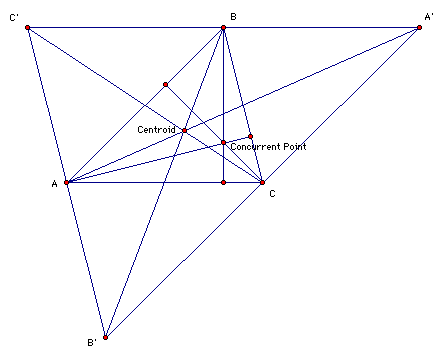
Unfortunately, the centroid and the orthocenter do not match in the current shape.

But is it possible to redraw the triangle so that the two points are equal?

Let's try it. Let's move point B to the left:

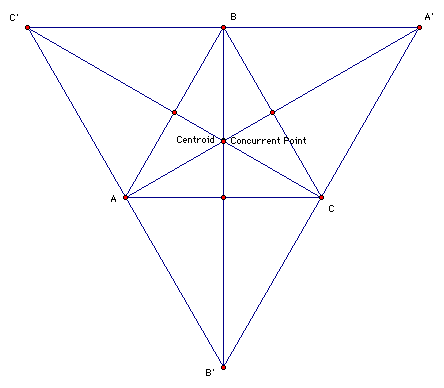We now have the centroid and the orthocenter being the same point.

Since the centroid is proven to be a point of concurrency for all triangles,

we have now proven that the orthocenter is a point of concurrency

for all triangles as well.

 

Return