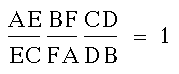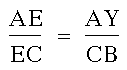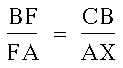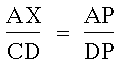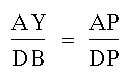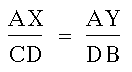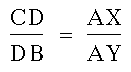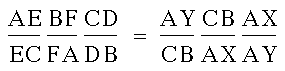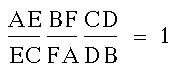Final Assignment
by Jeff Hall
Problem 1
Consider any triangle ABC. Select a
point P inside the triangle and draw lines AP, BP, and CP
extended to their intersections with
the opposite sides in points D, E, and F respectively.
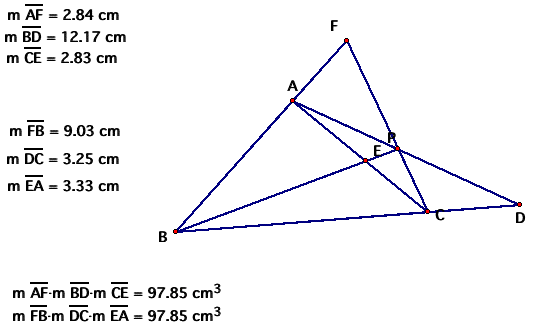
Here is the triangle described above:
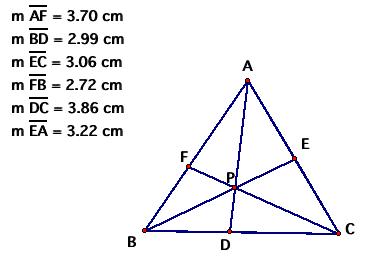 Explore (AF)(BD)(EC) and (FB)(DC)(EA)
for various triangles and various locations of P.
Explore (AF)(BD)(EC) and (FB)(DC)(EA)
for various triangles and various locations of P.
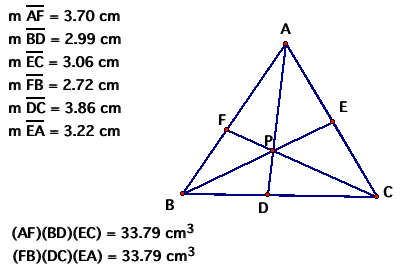 In this triangle configuration, the
products yielded the same measurement.
Let's try a different shaped triangle:
In this triangle configuration, the
products yielded the same measurement.
Let's try a different shaped triangle:
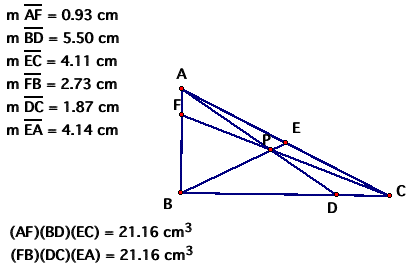 The different shape did not change
the fact that both products are the same.
Now let's try moving Point P to a different
location:
The different shape did not change
the fact that both products are the same.
Now let's try moving Point P to a different
location:
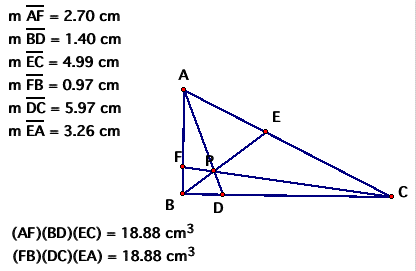 Once again, the products are the same,
regardless of the location of Point P.
Once again, the products are the same,
regardless of the location of Point P.
Problem 2
Conjecture? Prove it!
The three lines AD, BE, and CF are
concurrent according to Ceva's Theorem.
This theorem states that if the following
equation is true:
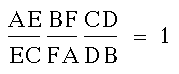 then the lines AD, BE, and CF are concurrent.
As we saw in problem 1, the products
were always equal to each other,
so their ratio is always 1.
To prove Ceva's Theorem, we can consider
similar triangles:
then the lines AD, BE, and CF are concurrent.
As we saw in problem 1, the products
were always equal to each other,
so their ratio is always 1.
To prove Ceva's Theorem, we can consider
similar triangles:
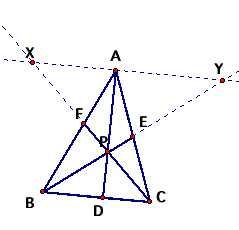 First, we create a line at Point A
parallel to Segment BC,
Then, we extend the lines BE and CF
to cross the parallel lines.
These new intersections are labeled
X and Y.
Triangle AYE is similar to CBE, so
we get:
First, we create a line at Point A
parallel to Segment BC,
Then, we extend the lines BE and CF
to cross the parallel lines.
These new intersections are labeled
X and Y.
Triangle AYE is similar to CBE, so
we get:
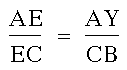 Triangles AFX and CBF are similar,
so we get:
Triangles AFX and CBF are similar,
so we get:
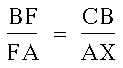 Triangles AXP and CDP are similar,
so we get:
Triangles AXP and CDP are similar,
so we get:
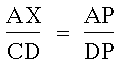 Triangles BDP and AYP are similar,
so we get:
Triangles BDP and AYP are similar,
so we get:
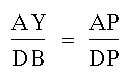 From these last two equations, we get:
From these last two equations, we get:
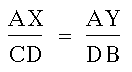 Therefore, we get this relationship:
Therefore, we get this relationship:
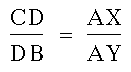 Multiplying this last equation and
the first two equations leads us to this:
Multiplying this last equation and
the first two equations leads us to this:
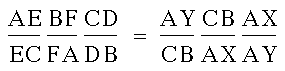 Since the equation on the right cancels
out to equal 1, we have demonstrated that
Since the equation on the right cancels
out to equal 1, we have demonstrated that
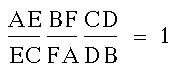 Therefore, the lines AD, BE, and CF
are concurrent.
What if Point P is outside of the Triangle,
like this?
Therefore, the lines AD, BE, and CF
are concurrent.
What if Point P is outside of the Triangle,
like this?
 As you can see, Ceva's Theorem still
holds.
Click here
if you would like to manipulate the triangle yourself.
As you can see, Ceva's Theorem still
holds.
Click here
if you would like to manipulate the triangle yourself.
Problem
3
Show that when P is inside triangle
ABC, the ratio of the areas of triangle ABC
and triangle DEF is always greater
than or equal to 4. When is it equal to 4?
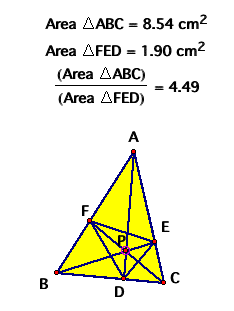 Moving Point P inside Triangle ABC
always generates a ratio greater than or equal to 4.
Moving Point P inside Triangle ABC
always generates a ratio greater than or equal to 4.
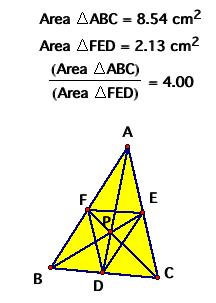 The ratio equals 4 at a many different
locations, but the following condition must hold true:
The ratios of the similar sides of
the two triangles must add up to 6, like so:
The ratio equals 4 at a many different
locations, but the following condition must hold true:
The ratios of the similar sides of
the two triangles must add up to 6, like so:

Return