

Problem 1.
x(n+1) = 3.2[x(n)][ 1 - x(n)]
Consider the behavior of the sequence for various x(0). Use a spreadsheet to display a table and graph for a sufficient range of n.
In particular, investigate the behavior of the sequence for x(0) in the range of
x(0) = .6875.
First, we evaluate the sequence for 0 and 1.
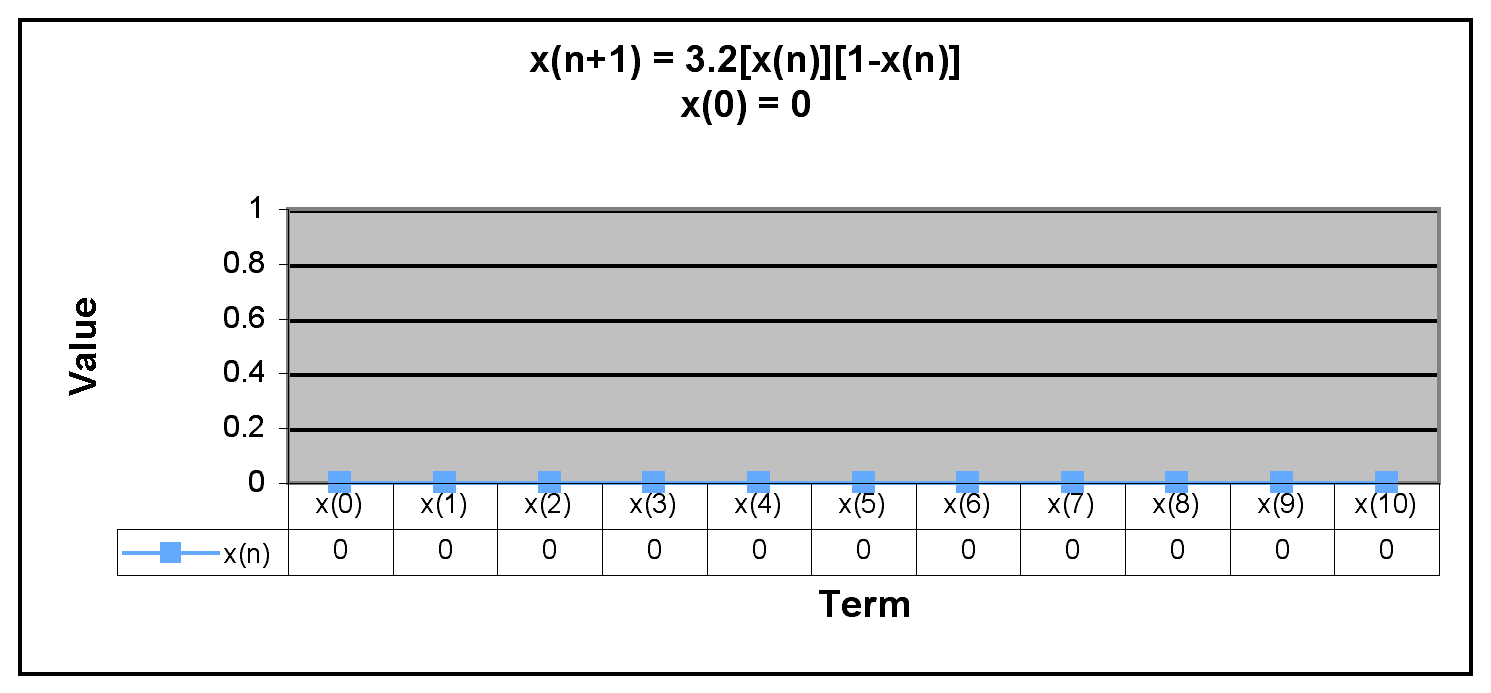
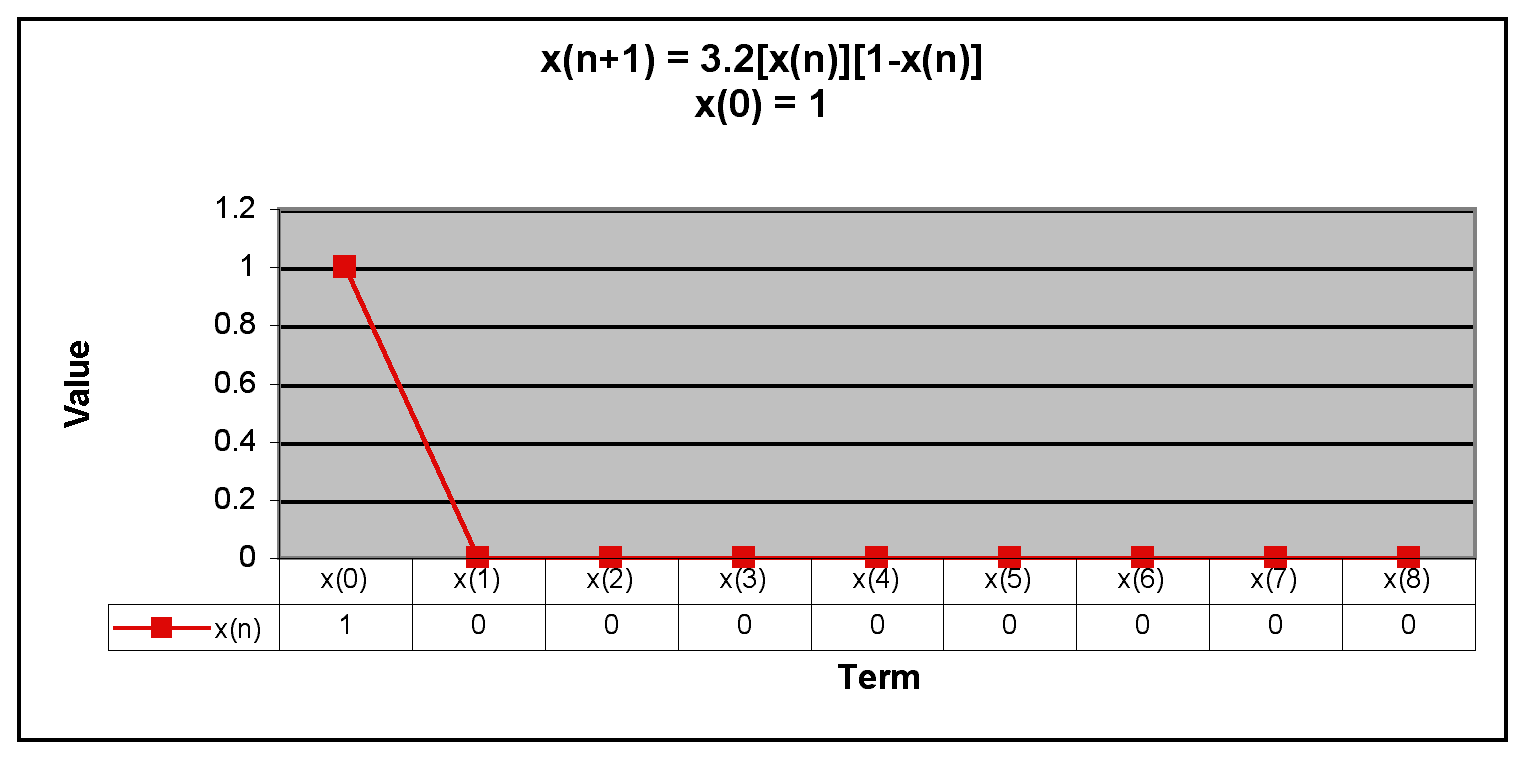
We can see from the graphs above that all x(n) are equal to 0 when x(0) = 0 and that all x(n) except x(0) equal zero when x(0) = 1.
Next, we examine when x(0) is equal to a number greater than 1.
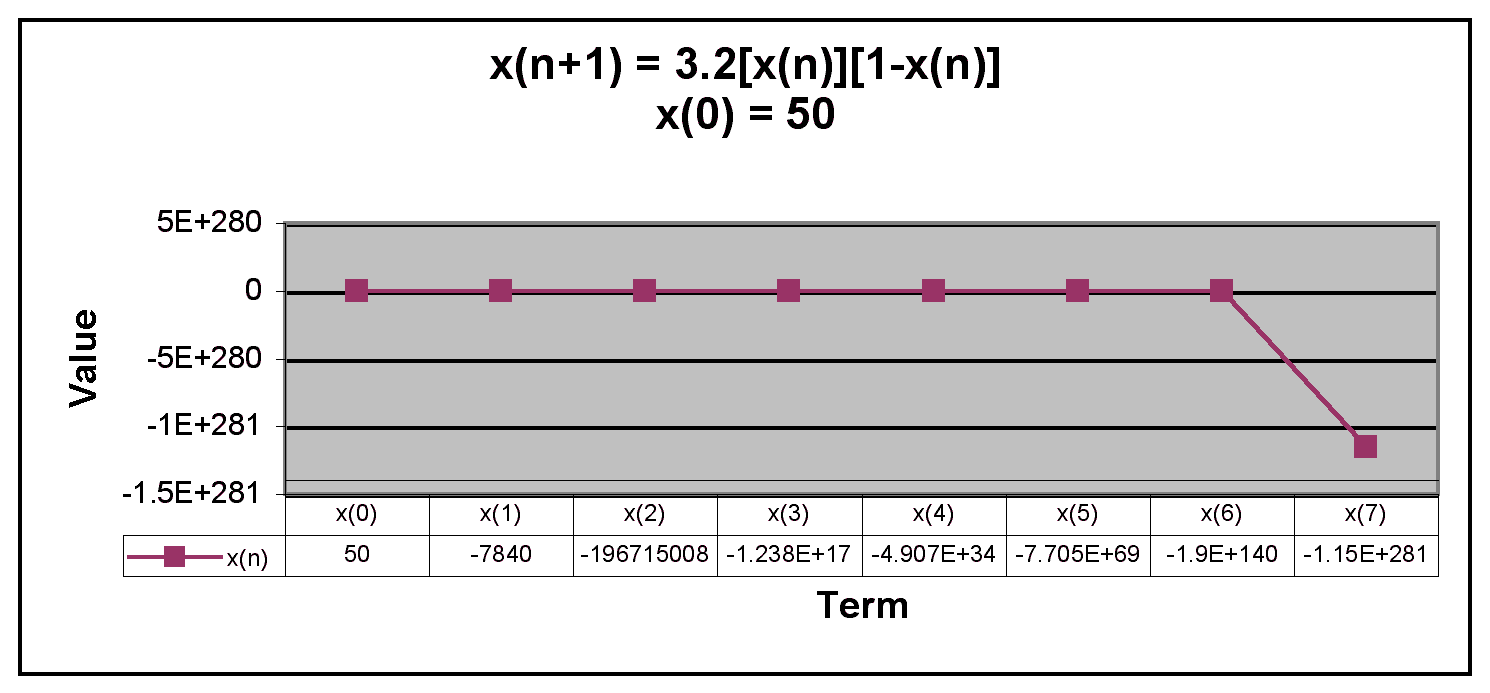
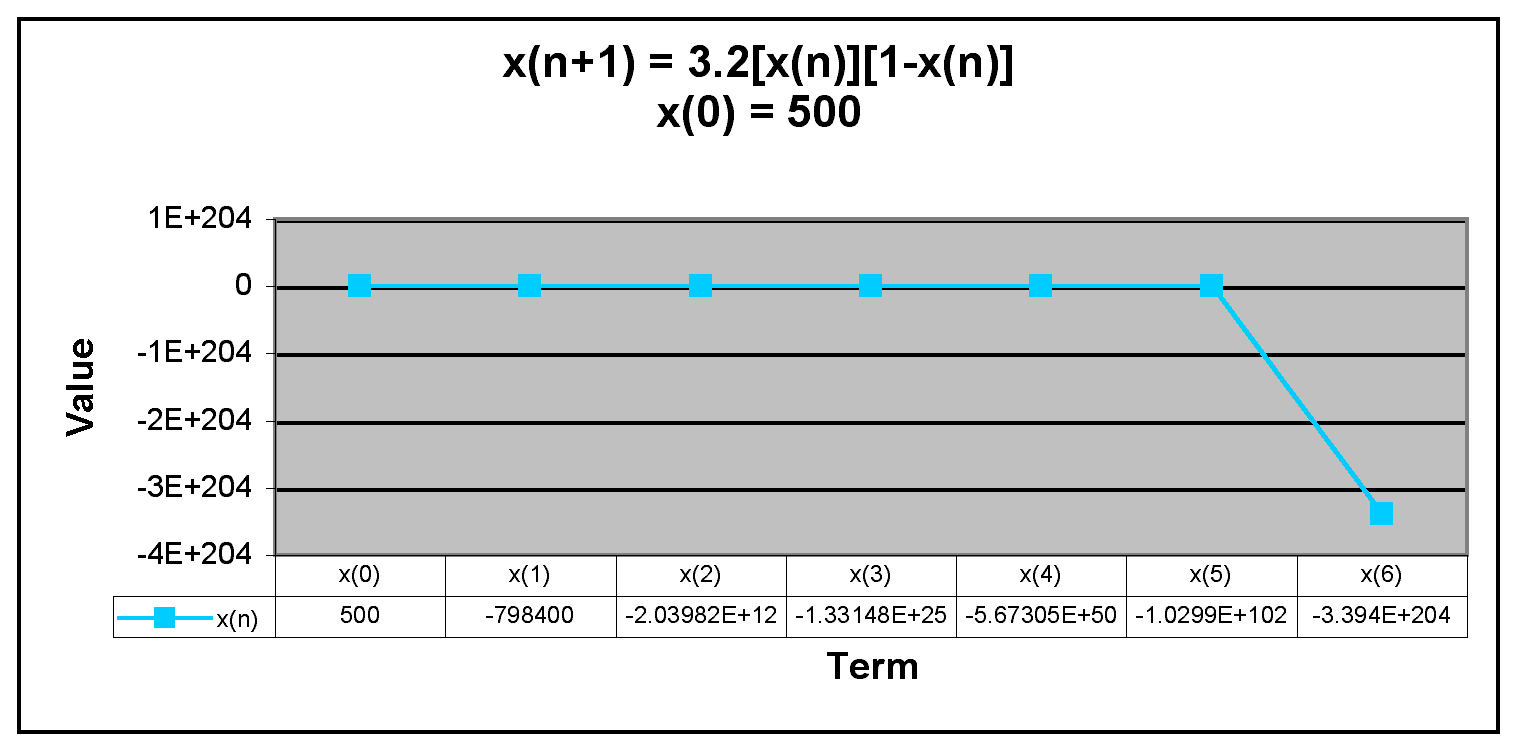
We can see from the graphs that x(n) decreases rapidly when x(0) is greater than 1. This was the result for all values greater than 1.
Next, we examine when x(0) is between 0 and 1.
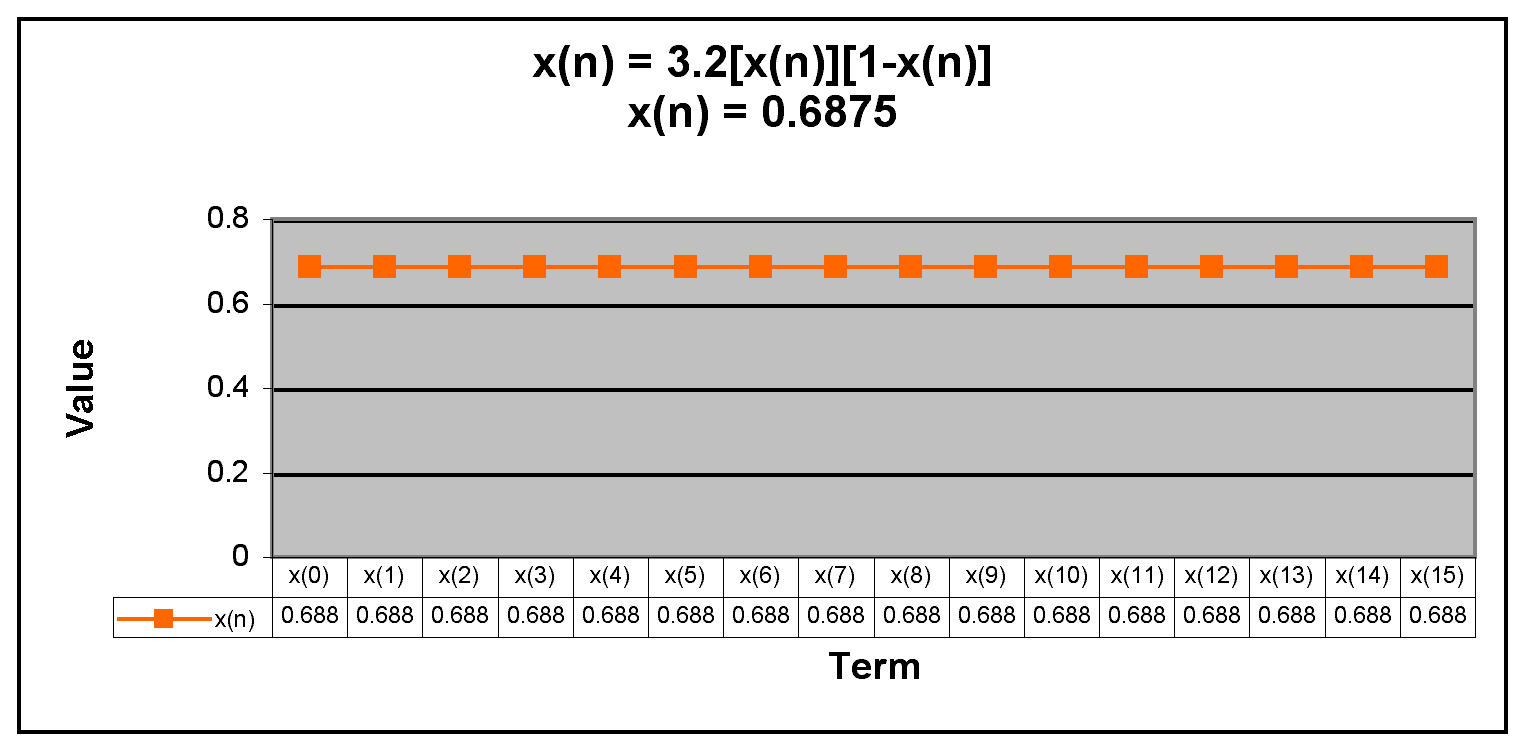
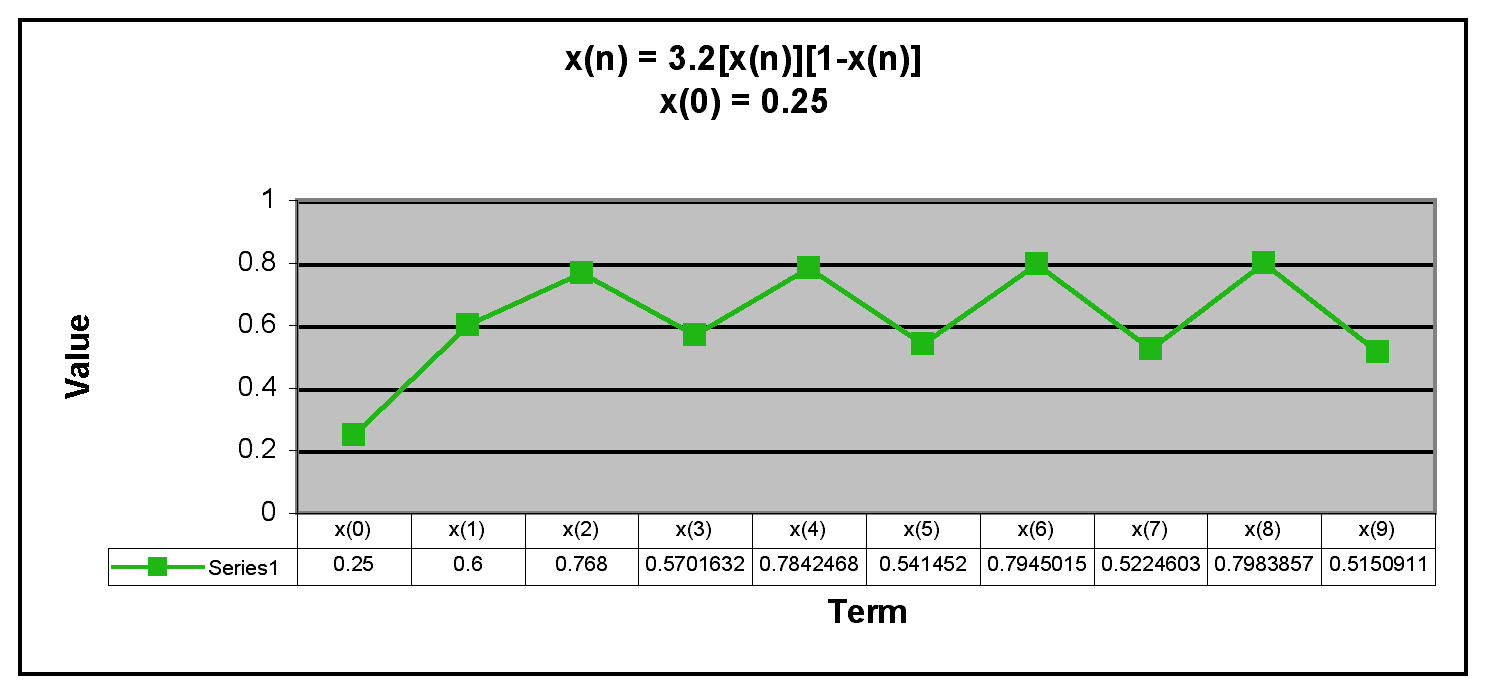
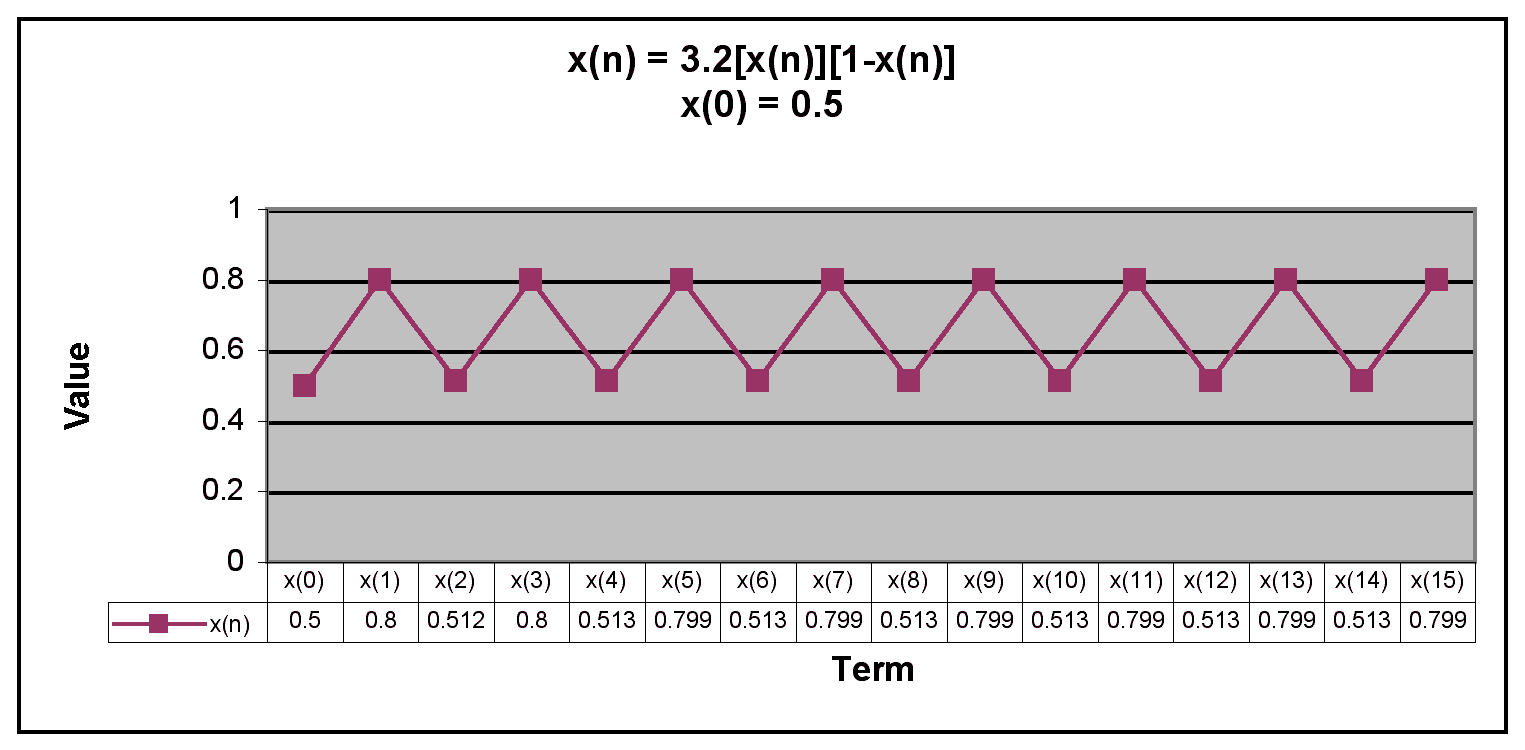
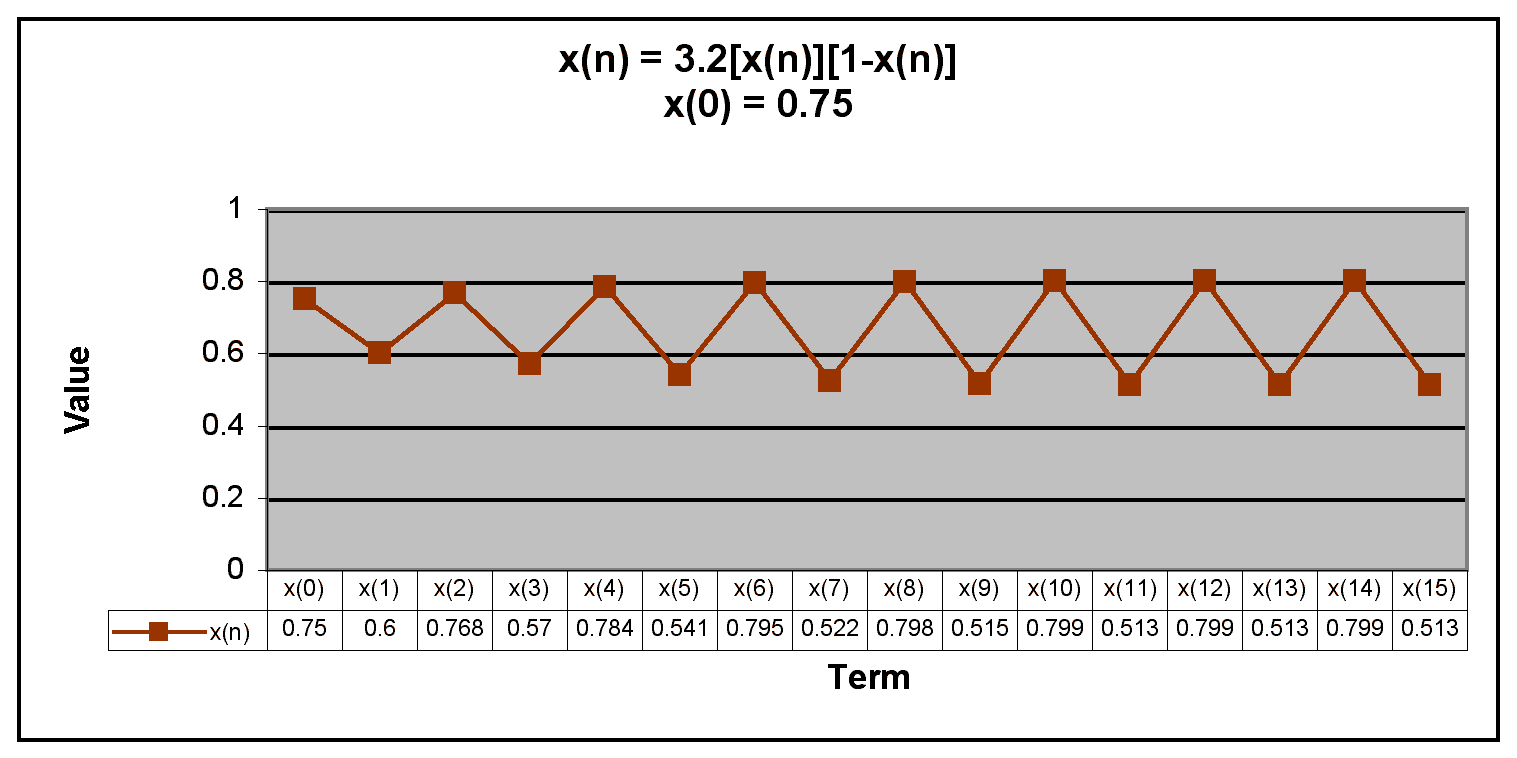
We notice that when x(0) = 0.6875, all of the terms in the sequence are equal to 0.6875. We also notice that for all other values of x(0) between 0 and 1, after the first few terms the sequence oscillates between two numbers.
Next, we examine negative values of x(0).
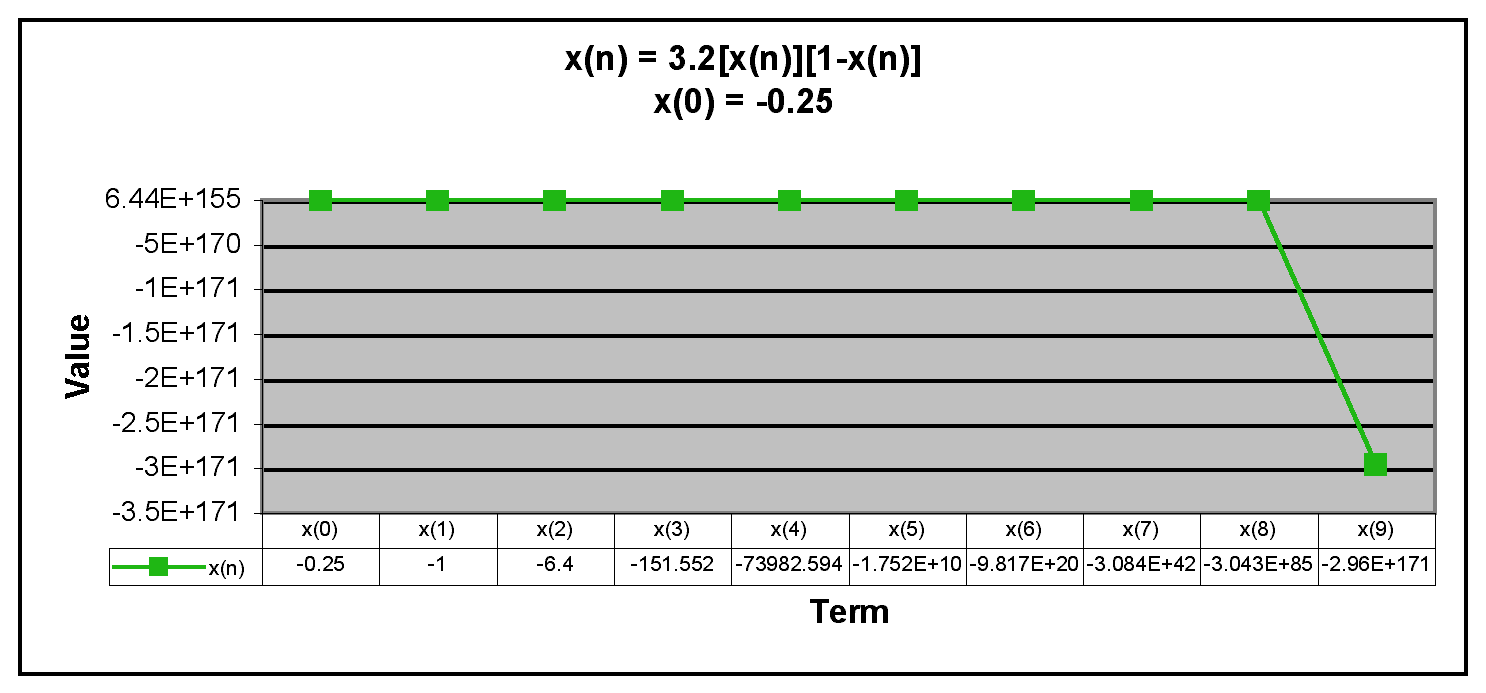
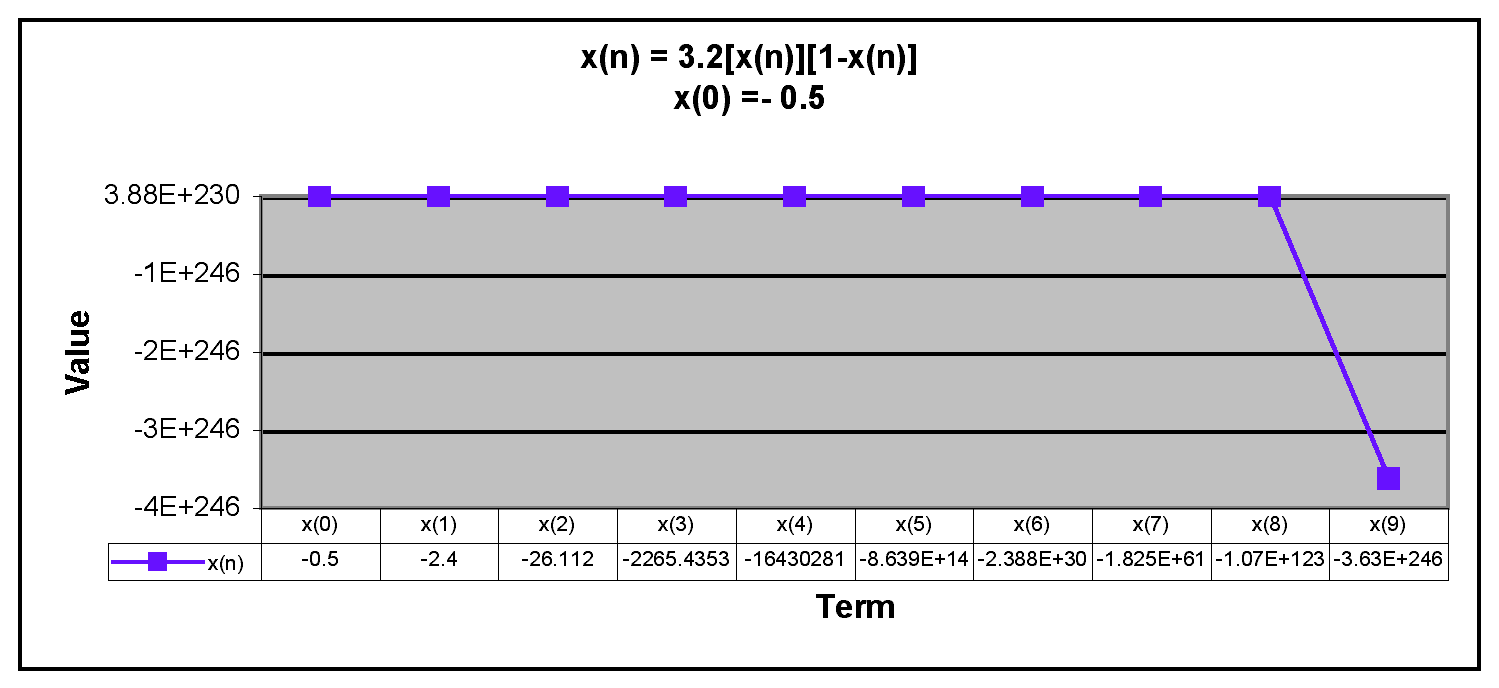
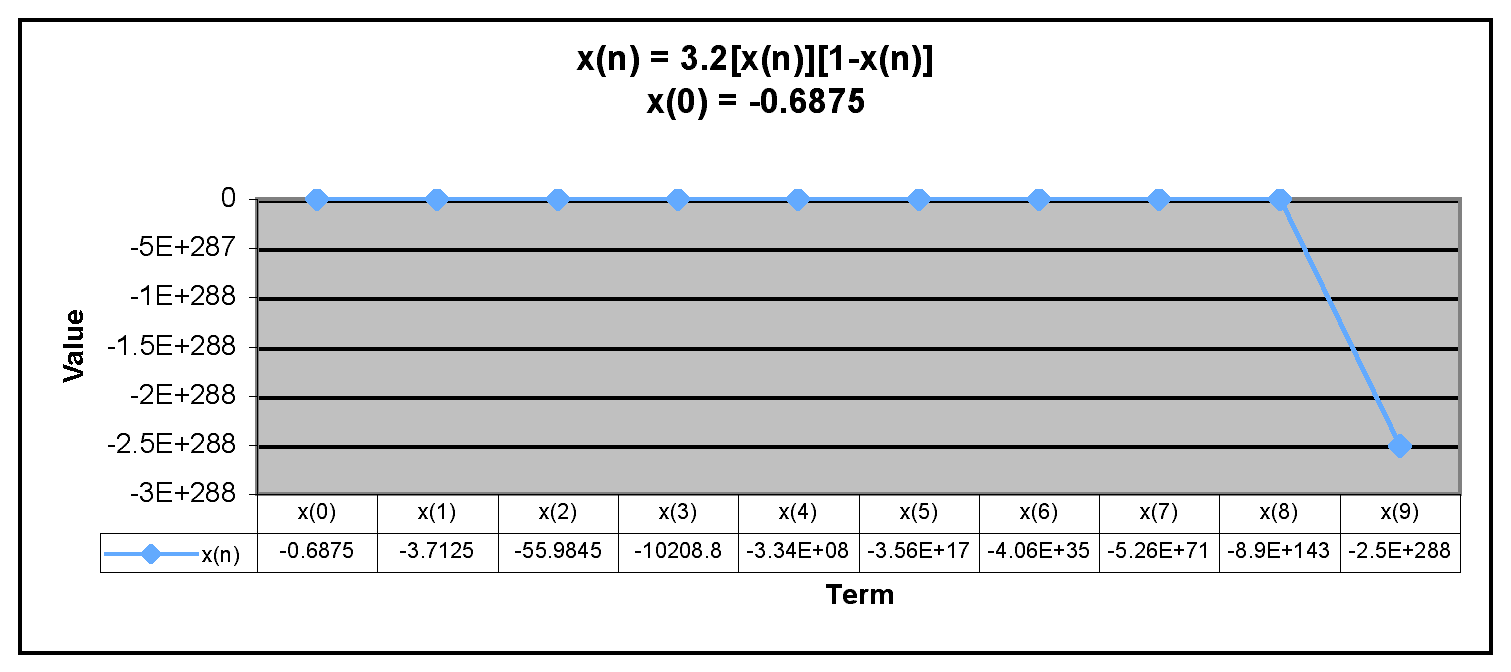
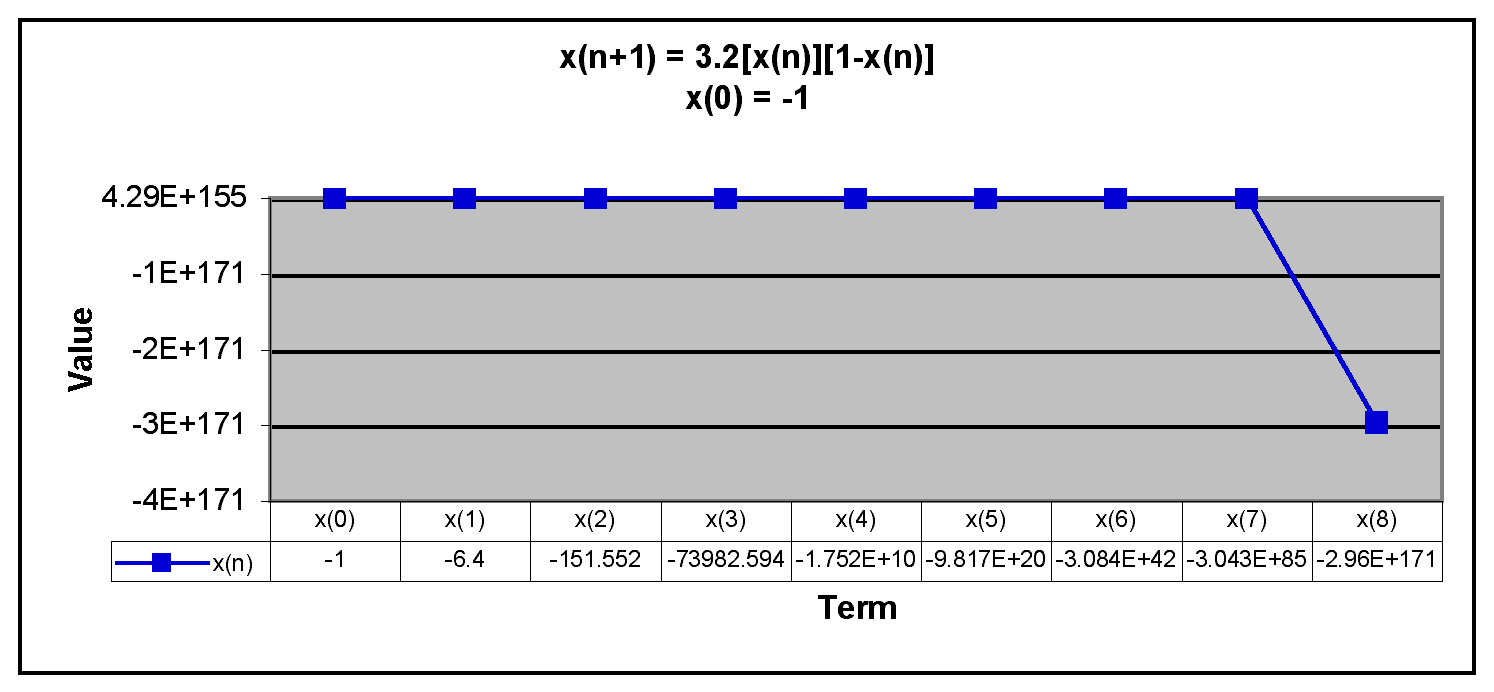
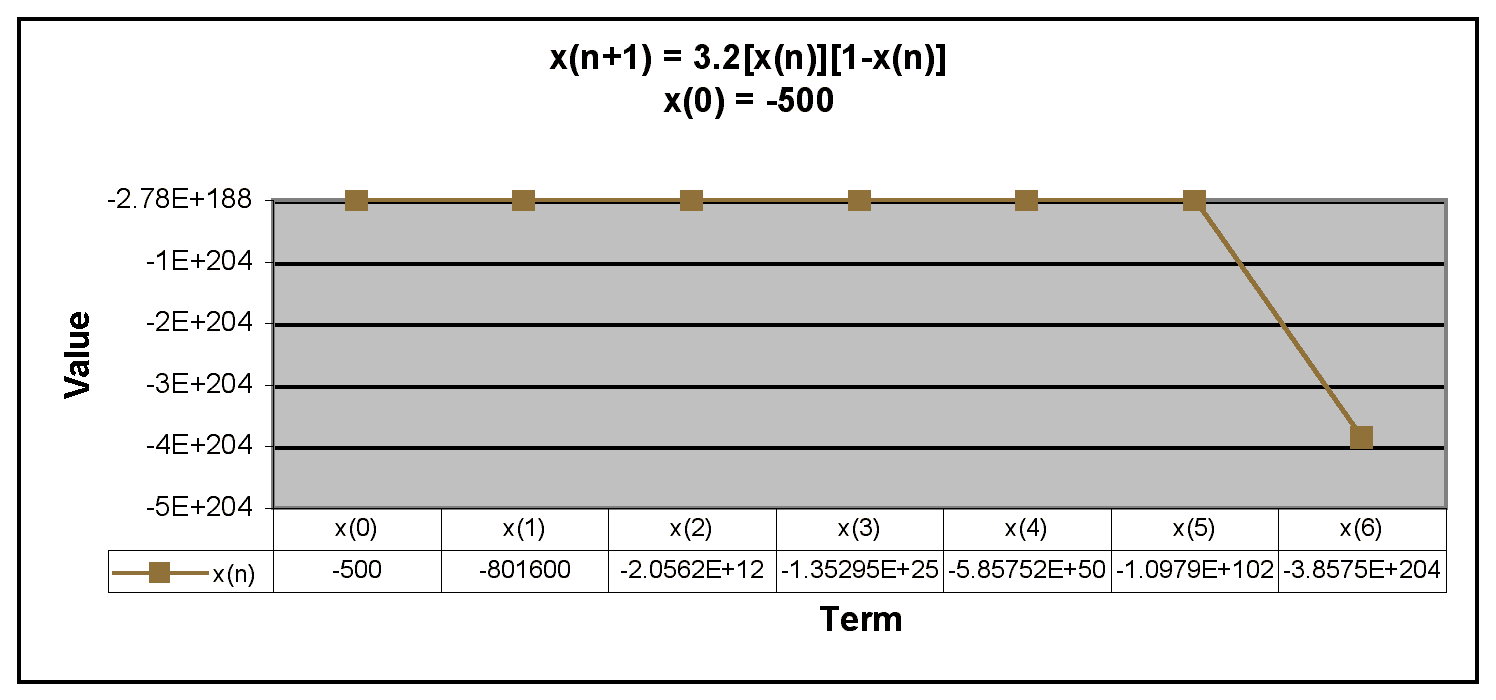
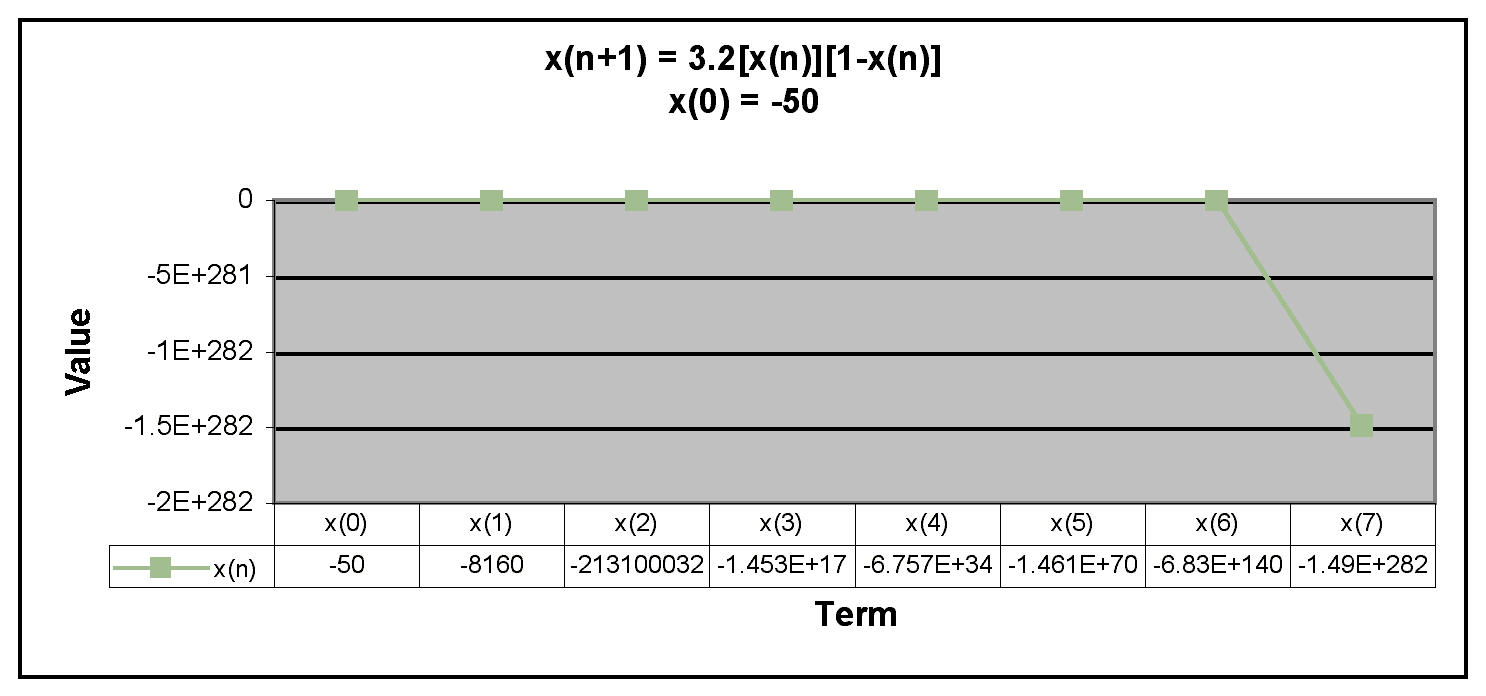
We can see from the graphs that when x(0) is negative, the terms in the sequence decrease rapidly. Thus, the sequence has the same behavior if x(0) is negative or greater than 1. The only time the sequence doesn't descrease rapidly is when x(0) is between 0 and 1.