

Problem 3.
Investigate with different values of p
For k > 1, k = 1, and k < 1.
First, let's examine the graph of
First, let's examine what happens when k = 1 and we change the value of p.
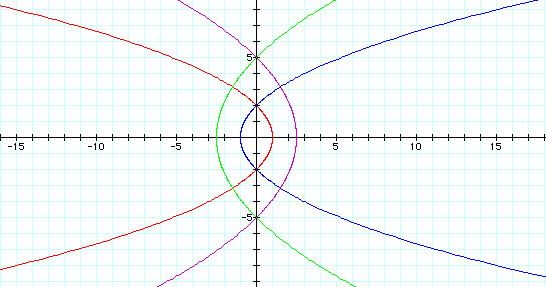
We notice that when k = 1 the graph is a parabola opening left or right. If p is positive, the graph opens to the right and if p is negative, the graph opens to the left. The greater the absolute value of p the wider the parabola.
Next, let's examine what happens when k > 1 and we change the
value of p. We will set k = 5.
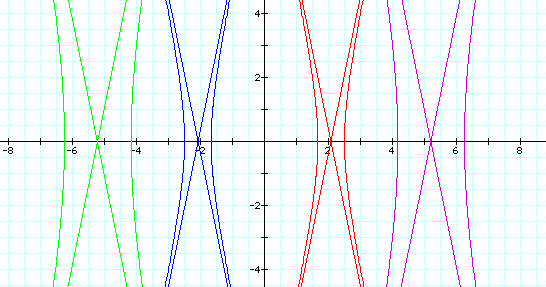
We notice that when k =5 the graph is
a hyperbola with lines at the asymptotes of the hyperbola. As
p gets larger, the graph moves to the right.
Next, let's examine what happens when k <1 and change the value of p. We will set k = -5.
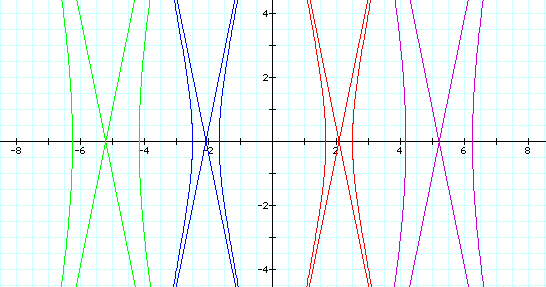
We notice that when k = -5 we get the same graph as k =5. It appears the graph is the same for positive and negative values of k.
Next, we will examine the graph of
First, let's examine what happens when k = 1 and we change the value of p.
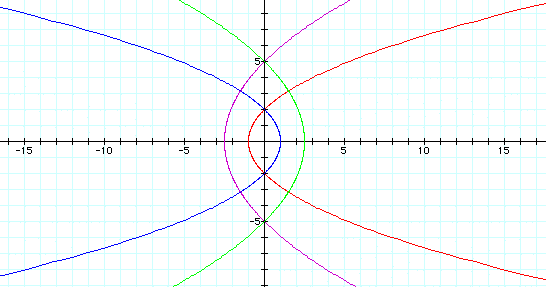
We notice that when k = 1 the graph is a parabola opening left
or right. If p is positive, the graph opens to the left and if
p is negative, the graph opens to the right. The greater the absolute
value of p the wider the parabola.
Next, let's examine what happens when k > 1 and we change the value of p. We will set k = 5.
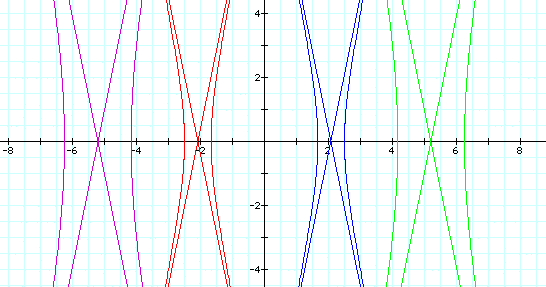
We notice that when k =5 the graph is
a hyperbola with lines at the asymptotes of the hyperbola. As
p gets larger, the graph moves to the left.
Next, let's examine what happens when k <1 and change the value of p. We will set k = -5.
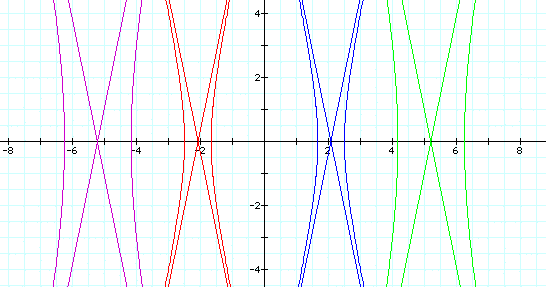
We notice that when k = -5 we get the
same graph as k =5. It appears the graph is the same for positive
and negative values of k.
Looking at these three graphs we notice that the graph of this
equation is a mirror image of the graph of the first equation.
Next, we will examine the graph of
First, let's examine what happens when k = 1 and we change the value of p.
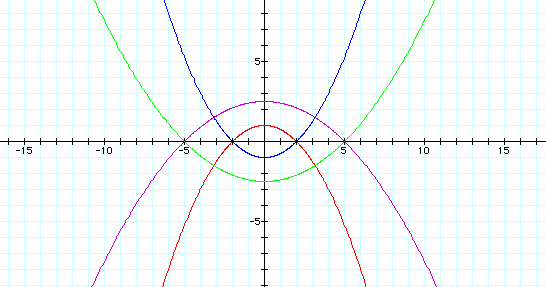
We notice that when k = 1 the graph is a parabola. If p is positive, the parabola opens up and if p is negative, the parabola opens down. The greater the absolute value of p the wider the parabola.
Next, let's examine what happens when k > 1 and we change the
value of p. We will set k = 5.
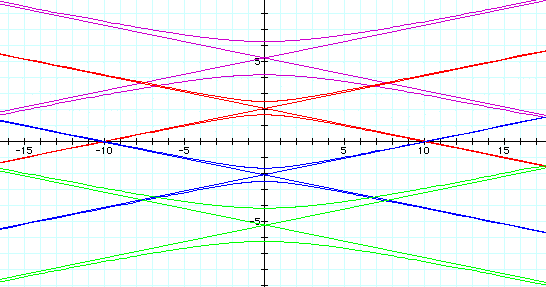
We notice that when k =5 the graph
is a hyperbola with lines at the asymptotes of the hyperbola.
As p gets larger, the graph moves down.
Next, let's examine what happens when k <1 and change the value of p. We will set k = -5.
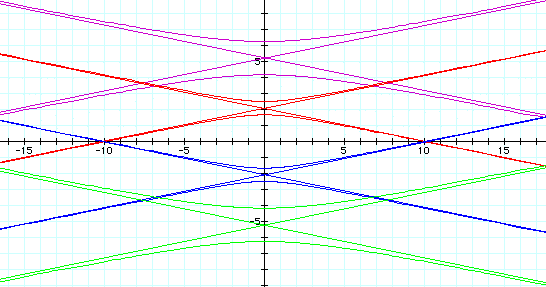
We notice that when k = -5 we get the
same graph as k =5. It appears the graph is the same for positive
and negative values of k.
Looking at these three graphs we notice that the graph of this
equation is a sideways image of the graph of the second equation.
Next, we will examine the graph of
First, let's examine what happens when k = 1 and we change the value of p.
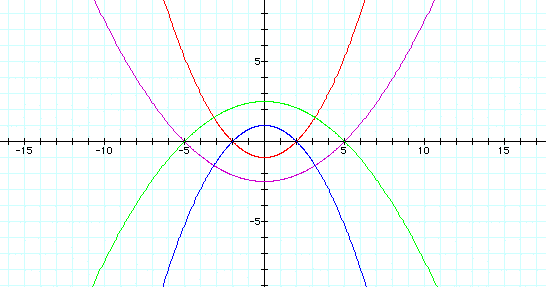
We notice that when k = 1 the graph is a parabola. If p is positive, the parabola opens down and if p is negative, the parabola opens up. The greater the absolute value of p the wider the parabola.
Next, let's examine what happens when k > 1 and we change the
value of p. We will set k = 5.
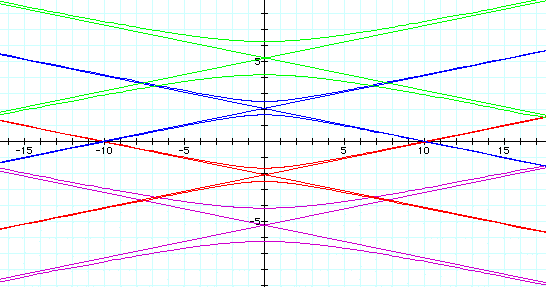
We notice that when k =5 the graph
is a hyperbola with lines at the asymptotes of the hyperbola.
As p gets larger, the graph moves up.
Next, let's examine what happens when k <1 and change the value of p. We will set k = -5.
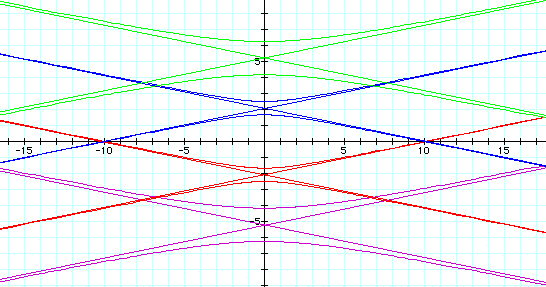
We notice that when k = -5 we get the
same graph as k =5. It appears the graph is the same for positive
and negative values of k.
Looking at these three graphs we notice that the graph of this
equation is a mirror image of the graph of the third equation.