

First we create triangle ABC. Then, we find the orthocenter H. Next ,we find the orthcenter of triangle HBC. We notice the orthocenter of triangle HBC is vertex A. Then, we find the orthocenter of triangle HAB, which we notice is vertex C. Last, we find the orthocenter of triangle HAC, which is vertex B.
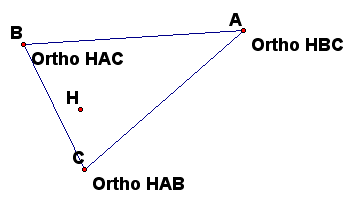
This is also true if H is not inside the triangle.
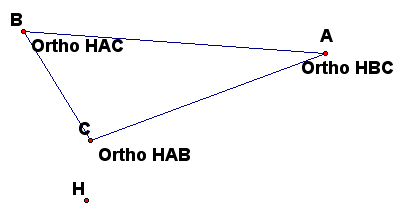
Here are pictures with the additional triangles shown.
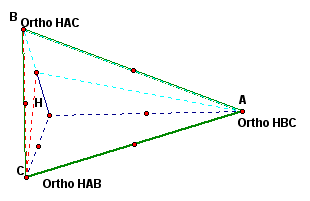
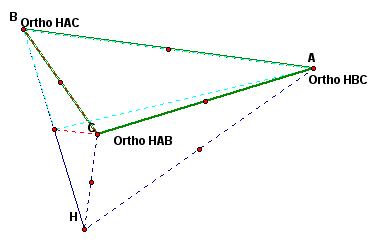
Next, we will construct the circumcircles and circumcenters of triangles ABC, HBC, HAB, and HAC.
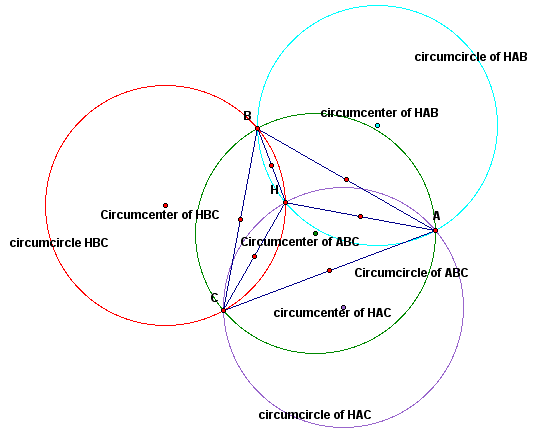
Here is the picture with the other triangles shown. The triangles overlap so they might be hard to see.
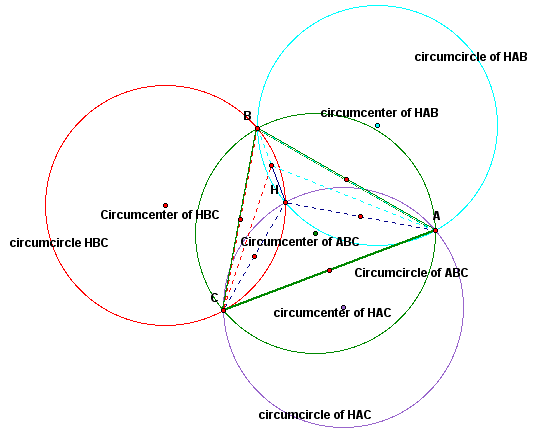
In the pictures above we have four triangles and four circumcircles. We notice the circumcircles of triangles HBC, HAB, and HAC all pass through point H. This makes sense because the circumcircle passes through all vertices in a triangle and all three of those triangles contain point H as a vertex. We also notice that each circumcircle intersects all the other circumcircles in two places.
Let's look at what happens if we move any vertex of the triangle to where H is located.
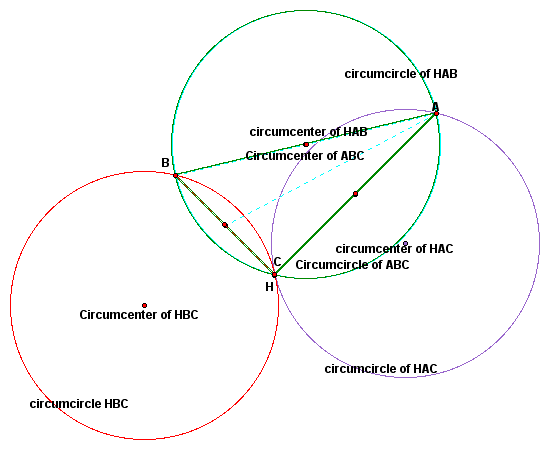
This picture demonstrates what happens when C is moved to H. We notice that triangle ABC is a right triangle and that H stays at point C. This means triangles ABC and HAB are now the same triangle. We also notice there are only three circumcircles instead of four. Since triangles ABC and HAB are the same triangle, the circumcenters and circumcircles are also the same.
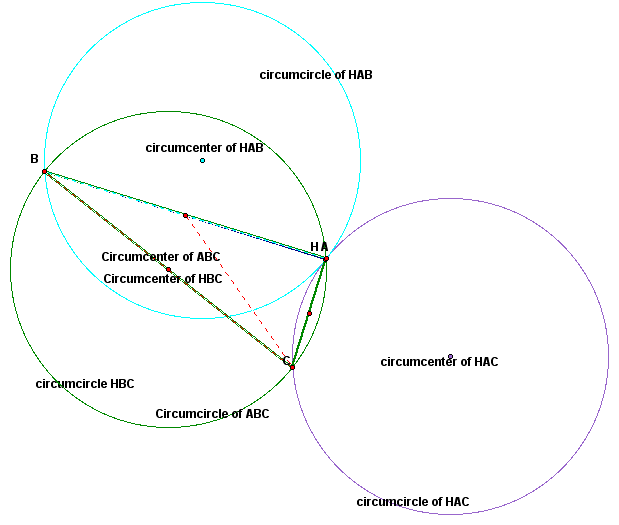
This picture demonstrates what happens when A is moved to H. We notice that triangle ABC is a right triangle and that H stays at point A. This means triangles ABC and HBC are now the same triangle. We also notice there are only three circumcircles instead of four. Since triangles ABC and HBC are the same triangle, the circumcenters and circumcircles are also the same.
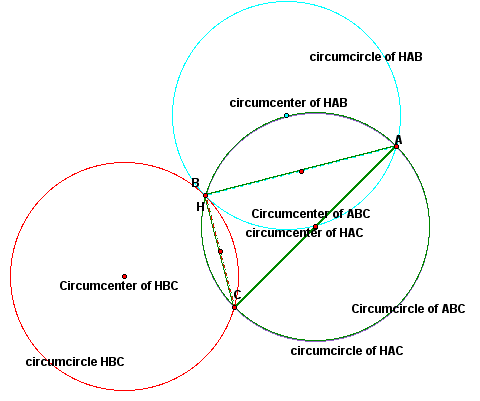
This picture demonstrates what happens when B is moved to H. We notice that triangle ABC is a right triangle and that H stays at point B. This means triangles ABC and HAC are now the same triangle. We also notice there are only three circumcircles instead of four. Since triangles ABC and HAC are the same triangle, the circumcenters and circumcircles are also the same.
One of the interesting facts regarding orthocenters noticed in the investigation is that the orthocenter of a right triangle is located at one of the vertices.