

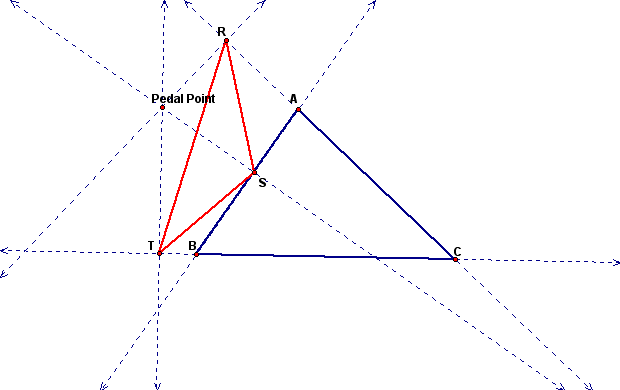
Let triangle ABC be any triangle and P be any
point in the plane, then construct the perpendiculars from point
P to the sides of ABC (extending the sides if needed). We will
call the three points of intersection R, S, and T. Triangle RST
is the Pedal triangle for the Pedal point P.
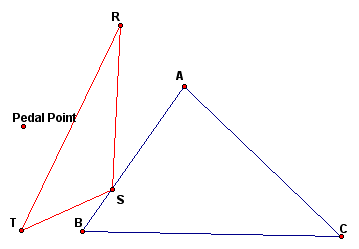
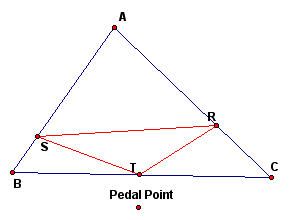
Here are some pictures of Pedal triangles (the first picture contains the construction lines).
Click here for a script tool to construct the Pedal triangle for a given triangle and a given Pedal point.
In the above pictures the Pedal point is any point in the plane. Next, we will investigate what happens when the Pedal point is the same as another special point for the triangle.
First, let's examine what happens when the Pedal point is the centroid of the triangle.
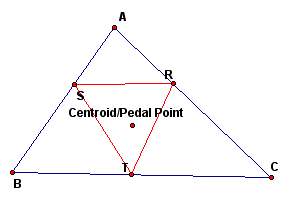
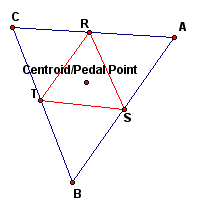
We notice that the Pedal triangle is always inside the triangle and acute (it appears to be equilateral but is not) when the Pedal point is the centroid.
Next, we examine what happens when the Pedal point is the incenter of the triangle.
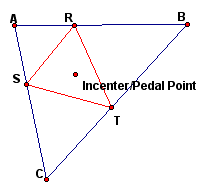
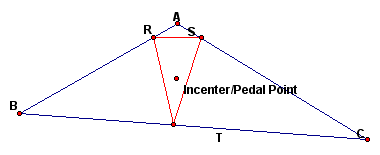
We notice that the Pedal triangle is always inside the original triangle and acute when the Pedal point is the incenter.
Next, we will examine what happens when the Pedal point is the orthcenter of the triangle.
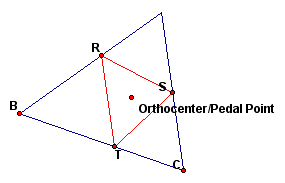
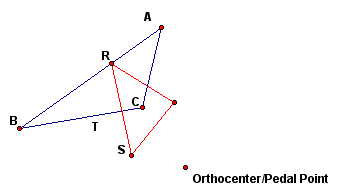
We notice that the Pedal triangle is inside the original triangle if the orthocenter is inside the triangle and the Pedal triangle overlaps the original triangle if the orthocenter is outside the triangle (if the original triangle is obtuse).
Next, we will examine what happens when the Pedal point is the circumcenter of the triangle.
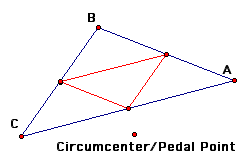
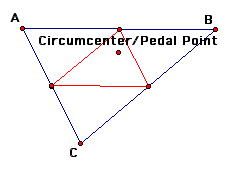
We notice that the Pedal triangle is always inside the original triangle regardless of if the circumcenter is inside or outside the original triangle.
Next, we will examine what happens when the Pedal point is on the side of a triangle.
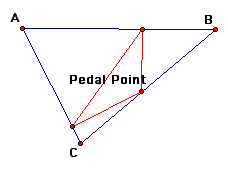
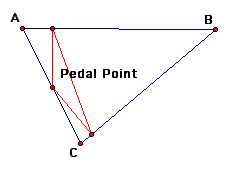
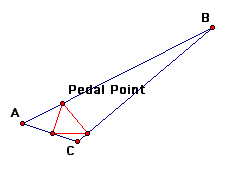
We notice that when the Pedal point is on a side of the triangle the Pedal triangle is always inside the original triangle.
Next, we will examine what happens when the Pedal point is one of the vertices of the original triangle.
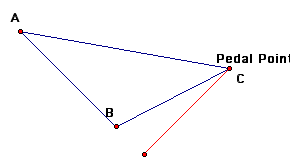
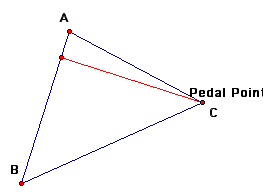
We notice when the Pedal point is one of the vertices of the original triangle the three vertices of the Pedal triangle are collinear (thus, it is a degenerate triangle).
Next, we will examine what happens when the Pedal point is on the circumcircle of the original triangle.
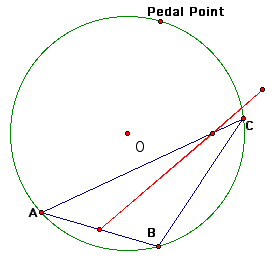
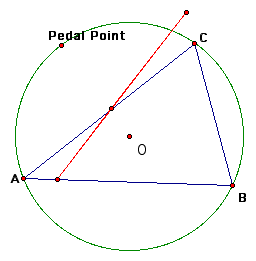
We notice when the Pedal point is located anywhere on the circumcircle the three vertices of the Pedal triangle are collinear (thus, it is a degenerate triangle).
The line segment created when the three vertices of the Pedal triangle are collinear is called the Simson Line. Here is a trace of the Simson Line as the Pedal point moves along the circumcircle.
