

Part A.
Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.
Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangle and various locations of P.
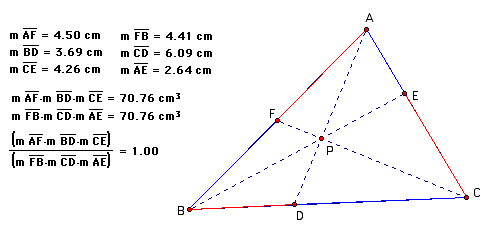
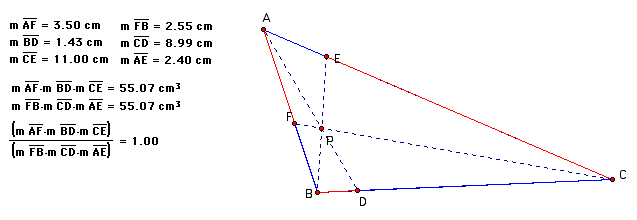
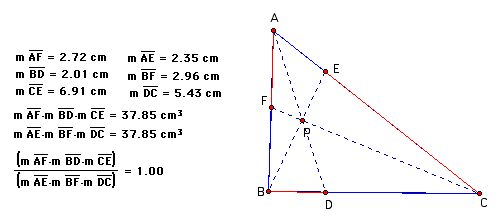
Click here to manipulate the GSP file.
Part B.
Conjecture: Regardless of what type of triangle or the location of P, the ratio of (AF)(BD)(EC) and (FB)(DC)(EA) seems to always be 1.
Prove it! (You may need to draw some parallel lines to produce similar triangles).
First, we will construct a line through P parallel to AC.
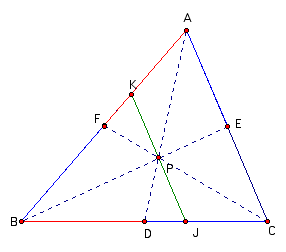

Next, we will construct a line through P parallel to BC.
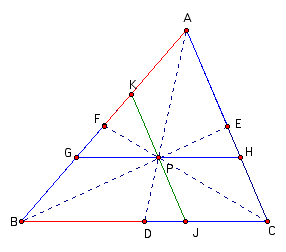
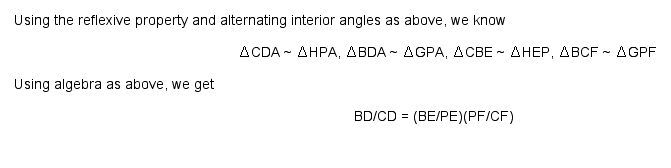
Next, we will construct a line through P parallel to AB.
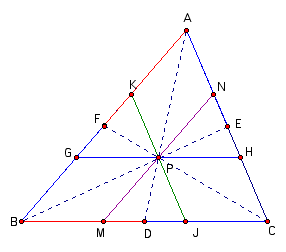
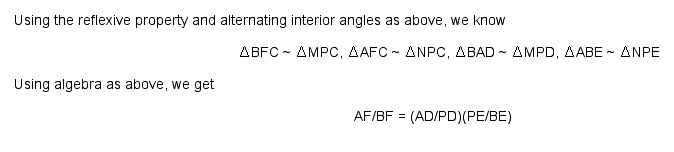
The last step is to substitute the values into the fraction
Can the result be generalized (using lines rather than segments to construct ABC) so that point P can be outside the triangle?
Here is a picture when P is outside of the triangle. Click here to open the GSP file.
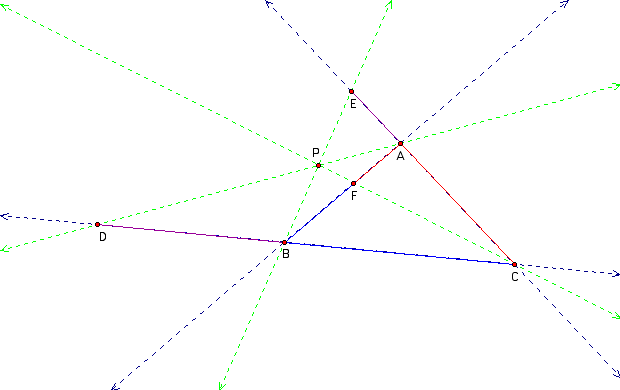
Even if P is outside the triangle, the similar triangles and proportions can be used to obtain the same result as above, so the relationship is still true.
Part C.
Show that when P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. When is it equal to 4?
Here are some instances of P inside the triangle with the ratio of the areas.
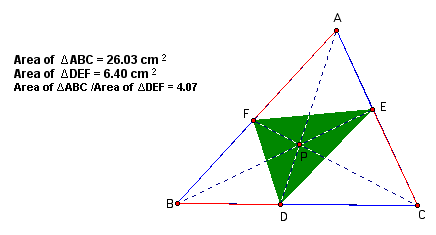
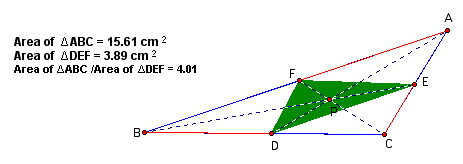
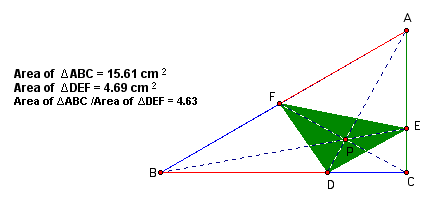
The ratio of the area is greater than or equal to 4 for an acute, obtuse, or right triangle.
Let's examine when the ratio of the areas of triangle ABC and triangle DEF is equal to 4.
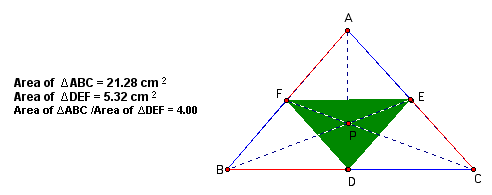
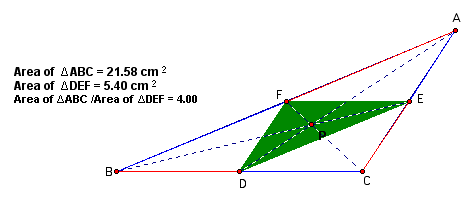
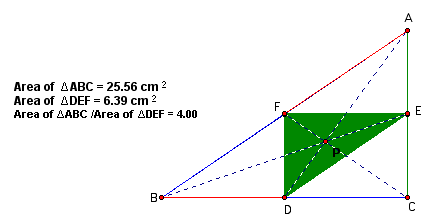
When the ratio of the areas of triangle ABC and triangle DEF is equal to 4 point P is located at the centroid of triangle ABC. We see this is true if the triangle is acute, right, or obtuse.