

For a pair of linear functions, f(x) and g(x), I wish to explore h(x) when
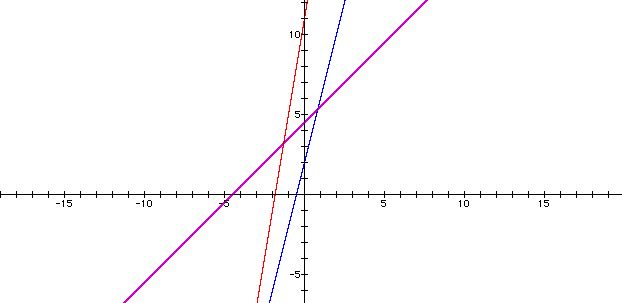
I begin with two linear functions, each having a positive slope:
In this instance, the sum is
The product is
The quotient is
The composite is
The graphs of f(x) and g(x) as well as the sum follow.
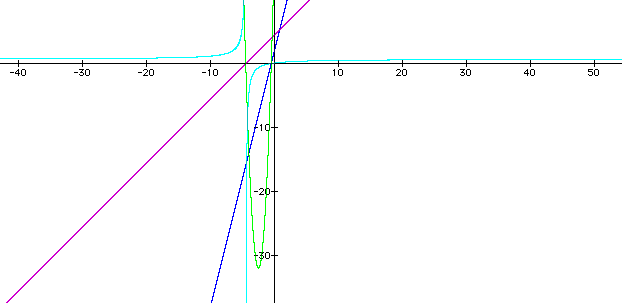
The green parabola is the graph of the product of f(x) and g(x) and the light blue hyperbola is their quotient.
In the final graph, the composite of f(x) and g(x) is shown overlayed on the graph of the two lines.
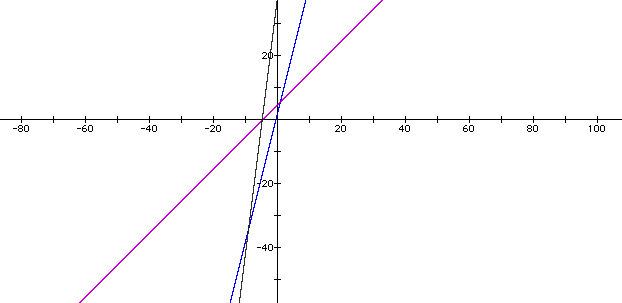
To view exploration of two linear functions, one with a positive slope and one with a negative slope, click here.
To view exploration of two linear functions having slopes that are multiplicative inverses, click here.
To view exploration of two linear functions
having slopes that are additive inverses, click here.
In examining the sums, products, quotients, and composites it is interesting to to investigate the domain and range of each of these new functions and well as to classify the new function.
The Sum
When h(x) = f(x) + g(x) where f(x) and g(x) are linear functions, h(x) will be a linear function with a domain of all real numbers as well as a range of all real numbers. The exception to this statement occurs when the slopes of f(x) and g(x) are additive inverses. In this instance, the sum is a constant and the range will be that particular constant.
The Product
In the instance where h(x) =f(x)*g(x), the resulting function will be quadratic. The domain of h(x) is all real numbers. The range is dependent on the slopes of f(x) and g(x) as well as the y coordinate of the vertex of the parabola. When both slopes are positive or both slopes are negative, the range will be all reals such that y is greater than or equal to the y coordinate of the vertex. When one slope is positive and the other is negative, the range will be all reals such that y is less than or equal to the y coordinate of the vertex.
The Quotient
When h(x) = f(x)/g(x) with f(x) and g(x) being linear functions, h(x) will have an asymptote occuring where g(x) = 0.
The Composite
For h(x)=f(g(x)), h(x) will always be a linear function with the domain being all real numbers and the range being all real numbers.
**It is also interesting to note that the leading coefficients of the product and the composite are the same for all pair of linear functions f(x) and g(x).