In this investigation, we begin by constructing a circle tangent to two given circles with one point of tangency being designated.

The following illustration shows the two given circles in blue and the tangent circle in red. In this instance, one of the given circles is completely inside the other.

---

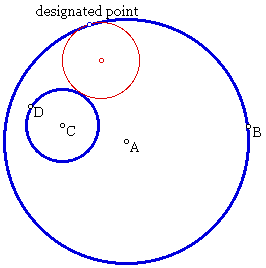
Now, let's look at the tangent circle (red) when the given circle intersect.

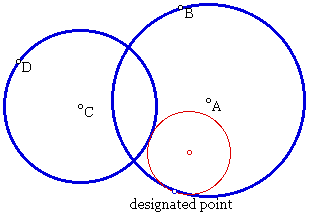
Notice that in this illustration, designated point has moved from the previous example. The tangent circle moves as this point moves.

Another interesting case occurs when the two given circles are disjoint.

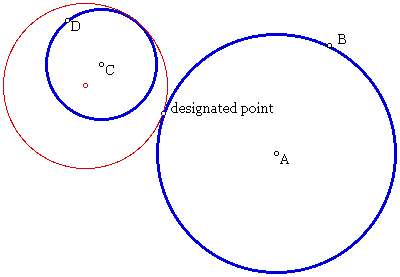
Here, we see that one of the given circles is now in the interior of the tangent circle.

At this point in our investigation, we may wonder what the locus (green) of the center of the tangent circle looks like. In our first example, with one of the given circle entirely inside the other.

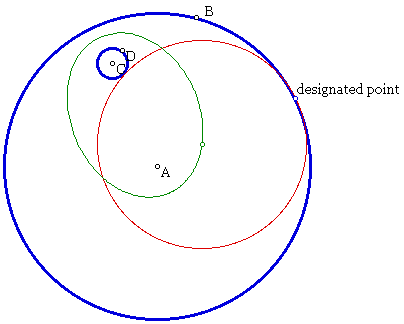
At this point, we notice that the locus is an ellipse with the foci being the centers of the original circles.

Now we wonder what the locus is when the circles are intersecting as in our second example.

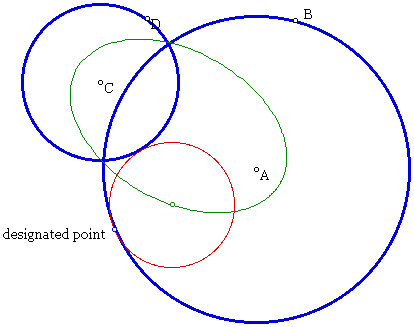
We quickly see that this locus is also an ellipse and that the centers of the original circles are the foci of the ellipse.

Now, we will investigate the situation shown in the third example with the two given circles being disjoint.

In this instance, we see that the locus of the center of the tangent circle is a hyperbola with the centers of the given circles acting as the foci.

To explore the pedagogical value of this assignment, click here.