

Given triangle ABC with medians CH, BF, and AG, we construct a triangle with the three sides having the lengths BF, CH, and AG. Now, we want to explore the relationship between the original triangle and the new one.
First, we find the perimeter and area of each triangle. Then, calculate the ratio of the new triangle to the original triangle in for both perimeter and area.
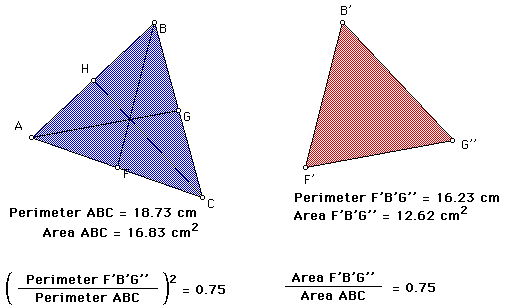
Notice that the ratio of the perimeters is not included, instead we see the ratio of the perimeters squared. Comparing this ratio to the ratio of the areas, we find that the ratios are equal. Will this relationship hold for any triangle and the triangle with its three sides the same length as the medians of the origianl triangle? Click here to try.
You will notice as you manipulate the original triangle, the ratio of the area remains constant at 0.75. Can you find instances where the ratio of the perimeters squared is not 0.75? The question to investigate becomes when is the ratio of the perimeters squared not 0.75?
If you would like to start with your own triangle, click here to run the script used in the example.