

The problem we will examine focuses on the triangle formed by the points of intersection of the extended altitudes of a given triangle ABC and the circumcircle of the same triangle (red triangle). We want to compare this red triangle (labeled altcircumtriangle in our calculations) to the orthic triangle (outlined in blue) of the original triangle ABC.
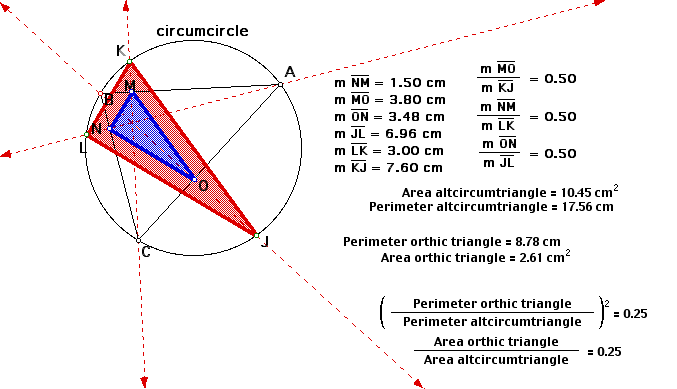
Focusing solely on the picture of the construction,
the two triangles in question appear to be similar. To quickly
verify this conjecture, we find the ratio of each pair of corresponding
sides. In each instance, the ratio is 0.50, indicating that the
triangles are indeed similar. Additionally, we can compare the
square of the ratio of the perimeters to the ratio of the areas.
We verify that these numbers are indeed the same, another fact
that is true of similar figures. It is of further interest to
note that the area of the orthic triangle is one fourth the area
of the triangle formed by the points of interestion of the extended
altitudes and circumcircle. To try this yourself, click
here.